La suite de Fibonacci

La suite de Fibonacci, du nom de Leonardo Fibonacci, également connu sous le nom de Leonardo de Pise, est une suite de nombres entiers fascinante qui a trouvé sa place dans divers domaines allant des mathématiques à l'architecture. Ce mathématicien italien du XIIIe siècle a introduit la suite de Fibonacci dans son ouvrage "Liber Abaci", un manuscrit qui a traversé le temps pour nous permettre de plonger dans les mystères de cette séquence particulière. À la croisée des mathématiques, de l'art et de la nature, la suite de Fibonacci est devenue une source d'inspiration inépuisable pour de nombreux domaines, illustrant la présence de motifs fascinants tels que la spirale d'or et la croissance exponentielle.
“On ne peut pas comprendre l'univers si l'on ne s'applique pas d'abord à en comprendre la langue et à connaître les caractères avec lesquels il est écrit. Il est écrit dans la langue mathématique.”

Qui est Leonardo Fibonacci ?
Leonardo Fibonacci (v. 1175 à Pise - v. 1250) est un mathématicien italien.
Il avait, à l'époque, pour nom d'usage « Leonardo Pisano » (il est encore actuellement connu en français sous l'équivalent de Léonard de Pise), et se surnommait parfois lui-même « Leonardo Bigollo » (bigollo signifiant « voyageur » en italien).
S'il est connu pour la suite de Fibonacci, il joue surtout un rôle d'une importance considérable en faisant le lien entre le savoir mathématique des Arabes, notamment des chiffres indo-arabes, et l'Occident.
Sa publication la plus connue reste très certainement le Liber abaci (aussi écrit Liber abbaci), publié en 1202.


Le livre des calculs est un traité sur les calculs et la comptabilité fondée sur le calcul décimal à une époque où tout l'Occident utilise encore les chiffres romains et calcule sur abaque. Ce livre est fortement influencé par son enfance vécue au sud et à l'est de la Méditerranée ; il est d'ailleurs rédigé en partie de droite à gauche.
Par cette publication, Fibonacci introduit en Europe le système de notation indo-arabe importé des Indes par les invasions arabo-musulmanes. Ce système est plus puissant et plus rapide que la notation romaine, et Fibonacci en est pleinement conscient.
L'invention sera d'abord mal reçue car le public ne comprend plus les calculs que font les commerçants. En 1280, Florence interdit même l'usage des chiffres arabes par les banquiers. On juge que le zéro apporte la confusion et des difficultés au point qu'ils appellent ce système cifra, qui dérive du nom arabe du zéro (al sifr = vide, zéro). Ce serait par l'usage des nombres dans la tradition cabalistique que le mot chiffre aurait acquis le sens de code secret.
Fibonacci est plus connu de nos jours pour un de ses problèmes conduisant aux nombres et à la suite qui portent son nom, mais à son époque, ce sont surtout les applications de l'arithmétique au calcul commercial qui l'ont fait reconnaître : calcul du profit des transactions, conversion entre monnaies de différents pays utilisant des bases différentes (base 10, 12, 20).
Son travail sur la théorie des nombres est ignoré de son vivant, mais il est très largement lu pendant les deux siècles suivants. Ses travaux sont désormais très utilisés en finance de marché, et en particulier en analyse technique.
Définition de la suite de Fibonacci
La suite de Fibonacci, notée Fib, débute par les deux premiers termes, 0 et 1, et chaque terme suivant est la somme des deux termes précédents, suivant la fonction Fib(n) = Fib(n-1) + Fib(n-2). On peut également exprimer la suite de Fibonacci via la formule mathématique, où le terme d'indice supérieur n est déterminé par la relation suivante. Ces premiers termes de la suite représentent le couple de lapins initial, symbolisant la croissance d'une population au fil des mois.
Un exemple d'application faisable de la suite de Fibonacci réside dans la modélisation de la croissance d'une population au cours des mois successifs, illustrant une progression suivant une suite arithmétique. L'évolution de cette suite peut être visualisée sous forme d'un quart de cercle, ou même utilisée pour répondre à des questions de divisibilité ou d'efficacité dans divers problèmes récréatifs. La suite de Fibonacci se ramifie également dans des domaines tels que l'architecture, où le rapport entre les côtés et les longueurs latérales suit une harmonie mathématique.
Léonard de Pise, l'auteur de nombreux manuscrits, a laissé un héritage indélébile avec la suite de Fibonacci, devenant une clé de l'harmonie dans la modélisation mathématique en dynamique, un petit poème numérique qui se dévoile bout à bout, et un modèle pour des figures biologiques, telles que la coquille de l'escargot. L'ensemble des suites, y compris le triangle de Pascal, s'entrelace avec la suite de Fibonacci, démontrant la profondeur de ses relations dans le vaste domaine des mathématiques.

Quelle est la loi dans la suite de Fibonacci ?
La suite de Fibonacci suit une loi de récurrence définie mathématiquement par la relation suivante:
F(n)=F(n−1)+F(n−2)F(n)=F(n−1)+F(n−2)
avec les conditions initiales F(0)=0F(0)=0 et F(1)=1F(1)=1. Cette relation exprime que chaque terme de la suite est la somme des deux termes précédents.
La formule explicite pour calculer le n-ème terme de la suite de Fibonacci sans avoir besoin de calculer tous les termes intermédiaires est également basée sur une loi mathématique, utilisant le nombre d'or (ϕ) :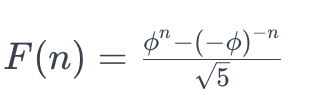
où ϕ est le nombre d'or, environ égal à 1.618033988749895.
La suite de Fibonacci présente également des propriétés intéressantes liées au nombre d'or et à la spirale d'or. Par exemple, à mesure que nn devient très grand, le rapport entre deux termes successifs de la suite de Fibonacci converge vers le nombre d'or (ϕ).
En résumé, la loi fondamentale dans la suite de Fibonacci est la relation de récurrence qui définit chaque terme en fonction des deux termes précédents. Cette loi simple génère une séquence de nombres qui présente des propriétés mathématiques fascinantes et qui trouve des applications dans divers domaines.
Quel est le lien entre le nombre d'or et la suite de Fibonacci ?
Le lien entre le nombre d'or (ou la spirale d'or) et la suite de Fibonacci est étroitement lié à la manière dont la suite de Fibonacci converge vers le nombre d'or à mesure que l'on progresse dans les termes de la séquence. Le nombre d'or, souvent représenté par la lettre grecque φ (phi), est une valeur irrationnelle d'environ 1,618033988749895. Ce nombre possède des propriétés mathématiques uniques, et il est souvent associé à des proportions esthétiques agréables dans l'art, l'architecture et la nature.
Le lien entre le nombre d'or et la suite de Fibonacci est illustré par la relation suivante : à mesure que l'on prend des termes successifs de la suite de Fibonacci et que l'on divise chaque terme par son prédécesseur, la valeur obtenue converge vers le nombre d'or. Formellement, cela peut être exprimé par la limite :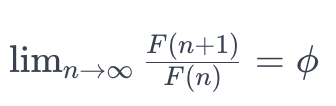
Dans cette équation, F(n)F(n) représente le n-ème terme de la suite de Fibonacci. Cette propriété de convergence crée des rapports de longueur agréables et des motifs géométriques qui sont souvent observés dans la nature et utilisés dans l'art et l'architecture. Par exemple, la spirale d'or, formée par l'ajout de carrés dont les côtés suivent la suite de Fibonacci, présente une croissance basée sur le nombre d'or, créant une spirale esthétiquement plaisante.
En résumé, le lien entre le nombre d'or et la suite de Fibonacci réside dans la convergence des rapports entre les termes successifs de la suite vers la valeur du nombre d'or, donnant lieu à des motifs harmonieux et esthétiques.
Dans la suite de Fibonacci, le rapport de tous deux termes successifs converge vers phi. Pourtant le mathématicien italien n’a jamais abordé spécifiquement le nombre d’or.
Pour visualiser ce phénomène, notons que chaque valeur successive de ce rapport se rapproche de plus en plus de phi :
1/1 = 1,000000
2/1 = 2,000000
3/2 = 1,500000
5/3 = 1,666667
8/5 = 1,600000
13/8 = 1,625000
21/13 = 1,615385
34/21 = 1,619048
55/34 = 1,617647
89/55 = 1,618182
144/89 = 1,617978
233/144 = 1,618056
377/233 = 1,618037
987/610 = 1,618033
En fait, 400 ans ont passé avant que Johannes Kepler établisse un lien explicite entre les deux. Il est le premier à mentionner clairement dans une lettre de 1609 que les rapports des termes successifs de la suite de Fibonacci se rapprochent du nombre d'or.
Quelle est la limite de la suite de Fibonacci ?
La suite de Fibonacci ne possède pas de limite finie, car ses termes augmentent indéfiniment à mesure que l'on progresse dans la séquence. Mathématiquement, on peut exprimer cela en disant que la limite de la suite de Fibonacci lorsque n tend vers l'infini n'existe pas en tant que nombre fini.
Formellement, la définition de la suite de Fibonacci est donnée par la relation de récurrence suivante : F(n)=F(n−1)+F(n−2)F(n)=F(n−1)+F(n−2), avec les conditions initiales F(0)=0F(0)=0 et F(1)=1F(1)=1.
Si l'on examine les termes de la suite, on constate qu'ils augmentent indéfiniment. Cela signifie que, à mesure que n devient de plus en plus grand, les valeurs de F(n)F(n) continueront à croître sans atteindre une limite finie.
En termes de notation mathématique, on peut exprimer cela en disant que :
![]()
Cela indique que la suite de Fibonacci diverge vers l'infini à mesure que n tend vers l'infini. C'est une caractéristique importante de cette séquence, et elle reflète la croissance exponentielle des termes de la suite.
Suite mathématique de Fibonacci : l’exemple des lapins
Dans son livre, Fibonacci présente aussi une suite numérique simple fondée sur un problème théorique de multiplication d'une population de lapins. Cette suite, la base d'une incroyable relation mathématique sous-tendant Phi, que les mathématiciens indiens connaissaient déjà au VIe siècle, a été introduite en Occident par Fibonacci.
La suite de Fibonacci peut être expliquée grâce à l'exemple suivant. Supposons deux lapins nouveau-nés, un mâle et une femelle. Supposons que les lapins sont capables de s'accoupler à l'âge de 1 mois, donc qu'à la fin de son deuxième mois de vie la femelle produira deux lapins. Supposons que nos lapins ne meurent jamais et que la femelle produit tous les mois, à partir de son deuxième mois de vie, deux autres lapins (un mâle, une femelle).
Fibonacci se demandait combien de lapins on finirait par avoir en une année. La réponse est 144, qui est le 12e nombre de la suite de croissance ci-dessous, correspondant au 12e mois de nouveaux lapins.

En partant de 0 et 1, chaque nouveau terme de la suite est simplement la somme des deux le précédant :
0 + 1 = 1
1 + 1 = 2
2 + 1 = 3
3 + 2 = 5
5 + 3 = 8
8 + 5 = 13
… etc., aboutissant à la suite suivante, portant le nom de Fibonacci :
0,1, 1, 2, 3, 5, 8, 13, 21,34, 55, 89, 144, 233, 377, 610, 987…
Spirale de Fibonacci
Si vous regardez sur internet des suites de Fibonacci, vous tomberez assurément sur des images de spirales de Fibonacci ou de spirales d'or. Vous avez vu aussi cette spirale superposée sur tout, du Parthénon à Mona Lisa, en passant par la naissance des cheveux de Donald Trump.
Typiquement, la spirale est créée en prenant pour base un rectangle d'or. Divisez le rectangle d'or en son point d’or et vous aurez un carré et un autre rectangle d'or plus petit. Faites pareil maintes fois avec le rectangle d'or plus petit pour créer l’image ci-dessous.
Et en y traçant un arc de cercle dans chaque carré on obtient la spirale d’or.


Pour une spirale apparentée, la spirale de Fibonacci, on utilise des carrés dont la longueur des côtés est égale aux termes de la suite de Fibonacci, au lieu de créer un motif successif de rectangles d'or.
Techniquement parlant, ce ne sont pas des spirales, mais des volutes. La différence est pratiquement imperceptible, mais une vraie est une spirale unique, équiangle (autrement dit, logarithmique), qui se développe à un rythme constant. Dans l’illustration ci-dessous, la spirale verte est construite par une succession d’arcs de cercles indépendants dans chaque carré. La spirale rouge est une vraie spirale logarithmique qui comporte le nombre d'or tous les 90 degrés (spirale équiangulaire). Les parties qui se superposent sont en jaune.

A quoi sert et quand utiliser la suite de Fibonacci ? Les applications.
La suite de Fibonacci a une grande importance dans divers domaines et est utilisée à des fins variées.
Voici quelques-unes des applications et utilisations de la suite de Fibonacci :
• Modélisation de la croissance et de la population : La suite de Fibonacci peut être utilisée pour modéliser la croissance d'une population, en particulier dans des situations où chaque génération dépend des générations précédentes.
• Analyse financière : Certains aspects de la suite de Fibonacci sont utilisés dans l'analyse technique des marchés financiers pour identifier des niveaux de support et de résistance potentiels.
• Art et design : La spirale d'or, qui est liée à la suite de Fibonacci, est utilisée dans l'art et le design pour créer des proportions esthétiquement agréables. Des artistes et architectes ont incorporé ces proportions dans leurs œuvres pour créer une harmonie visuelle.
• Informatique et algorithmes : La suite de Fibonacci est utilisée dans le domaine informatique, en particulier pour des algorithmes récursifs et des problèmes de programmation dynamique. La fonction fib est souvent utilisée comme exemple pour enseigner la récursivité en informatique.
• Cryptographie : Certains algorithmes cryptographiques utilisent des propriétés de la suite de Fibonacci pour générer des nombres aléatoires.
• Biologie : Certains modèles biologiques s'appuient sur la suite de Fibonacci pour décrire la croissance de certaines structures, comme les pétales de fleurs ou les coquilles d'escargots.
• Mathématiques pures : La suite de Fibonacci est étudiée en mathématiques pures pour comprendre ses propriétés et ses comportements. Elle est également utilisée pour illustrer divers concepts mathématiques aux étudiants.
En résumé, la suite de Fibonacci n'a pas seulement une signification mathématique, mais elle trouve des applications dans de nombreux domaines, de l'art à la biologie, en passant par la finance et l'informatique. Son omniprésence démontre la beauté et la polyvalence de cette séquence numérique.
La suite de Fibonacci dans la nature
La suite de Fibonacci est fréquemment observée dans la nature, illustrant comment les modèles mathématiques peuvent se manifester dans le monde vivant. Plusieurs exemples démontrent la présence de cette séquence dans diverses structures biologiques, formes et phénomènes naturels. Voici quelques exemples de la suite de Fibonacci dans la nature :
• Disposition des feuilles sur une tige : Dans de nombreuses plantes, la disposition des feuilles sur une tige suit la suite de Fibonacci. Les feuilles poussent généralement de manière à maximiser l'exposition à la lumière solaire et à éviter l'ombre des feuilles voisines, créant ainsi une disposition en spirale conforme à la suite de Fibonacci.
• Spirales dans les pommes de pin : Les spirales présentes sur les pommes de pin suivent souvent la suite de Fibonacci. Les graines sont disposées en spirales de manière à maximiser l'espace tout en maintenant une distribution uniforme.
• Coquilles d'escargots et de mollusques : Les coquilles de certains escargots et mollusques suivent la forme d'une spirale logarithmique, qui est liée à la suite de Fibonacci. Cette structure permet à l'animal de créer une coquille de manière efficace tout en assurant une croissance continue.
• Fleurs et pétales : Le nombre de pétales dans de nombreuses fleurs suit souvent des séquences de Fibonacci. Par exemple, les marguerites peuvent avoir 21, 34, ou 55 pétales, nombres qui correspondent à des termes successifs de la suite de Fibonacci.
• Ramification des arbres : La ramification des branches d'arbres peut également suivre des motifs basés sur la suite de Fibonacci. Les branches se divisent de manière à maximiser l'efficacité de la capture de la lumière solaire.
• Écailles de certains fruits et légumes : La disposition des écailles sur certains fruits, tels que l'ananas, suit parfois la suite de Fibonacci, créant des motifs géométriques intéressants.
La présence de la suite de Fibonacci dans ces structures naturelles suggère que cette séquence numérique offre des solutions optimales pour des processus de croissance et de distribution dans le règne végétal et animal. Cela témoigne de la beauté des mathématiques dans la conception de la nature.



La suite de Fibonacci dans l'art et l'architecture
La suite de Fibonacci et ses propriétés mathématiques influencent également le domaine artistique, où elle est utilisée pour créer des œuvres esthétiquement plaisantes et harmonieuses. Les artistes ont exploré la présence de la suite de Fibonacci dans diverses formes d'art, allant de la peinture à la sculpture en passant par l'architecture. Voici quelques façons dont la suite de Fibonacci s'exprime dans l'art :
• Proportions et ratios : Les proportions basées sur la suite de Fibonacci, notamment le nombre d'or, sont souvent utilisées pour déterminer la taille et la disposition d'éléments dans une œuvre d'art. Ces ratios sont considérés comme esthétiquement agréables et ont été utilisés dans des compositions artistiques célèbres.
• Spirales d'or : La spirale d'or, dérivée de la suite de Fibonacci, est utilisée dans la création de motifs spiraloïdes dans l'art. Des artistes ont incorporé ces spirales dans des peintures, des sculptures et des œuvres graphiques pour créer une dynamique visuelle harmonieuse.
• Mosaïques et carrelages : Certains motifs de mosaïques et de carrelages suivent les proportions de la suite de Fibonacci. Ces motifs créent un effet visuel agréable et sont utilisés dans l'art décoratif, l'architecture et la conception d'intérieur.
• Fresques et peintures murales : Des artistes utilisent la suite de Fibonacci pour déterminer la taille des éléments dans des fresques et des peintures murales, créant ainsi des compositions équilibrées et esthétiquement satisfaisantes.
• Photographie et composition visuelle : Les photographes utilisent parfois la suite de Fibonacci pour composer des images de manière à attirer l'œil et créer une harmonie visuelle. Des proportions basées sur la suite de Fibonacci peuvent être appliquées pour guider le spectateur à travers une image.
• Architecture : Certains architectes intègrent la suite de Fibonacci dans la conception de bâtiments et de structures. Les proportions basées sur la suite de Fibonacci peuvent être utilisées pour déterminer la hauteur des étages, la largeur des fenêtres et d'autres éléments architecturaux.
L'utilisation de la suite de Fibonacci dans l'art démontre comment les concepts mathématiques peuvent inspirer la création artistique et contribuer à la perception visuelle. Cela offre aux artistes un cadre structuré pour exprimer la beauté et l'harmonie dans leurs œuvres.

La suite de Fibonacci dans la musique
Bien que la suite de Fibonacci ne soit pas directement utilisée dans la composition musicale de la même manière que dans les mathématiques, son influence se manifeste à travers des concepts et des structures harmoniques. Les musiciens et compositeurs ont parfois exploré des idées liées à la suite de Fibonacci pour créer des motifs et des structures dans la musique. Voici quelques façons dont la suite de Fibonacci peut être présente dans la musique :
• Rythmes et durées : Certains compositeurs expérimentent avec des motifs rythmiques basés sur la suite de Fibonacci. Les durées des notes peuvent suivre des séquences qui rappellent la progression de la suite, ajoutant une dimension mathématique à la structure rythmique.
• Structures de compositions : Certains musiciens ont utilisé les principes de la suite de Fibonacci pour déterminer la structure de leurs compositions. Par exemple, la disposition des sections d'une œuvre musicale peut suivre des proportions basées sur la suite de Fibonacci, créant ainsi une progression harmonique et mélodique intéressante.
• Fréquences et intervalles : Les relations harmoniques dans la musique, telles que les rapports d'intervalles entre les notes, peuvent être influencées par des concepts mathématiques tels que la suite de Fibonacci. Bien que cela puisse ne pas être toujours explicite, la quête de consonance et de dissonance dans la musique peut être liée à des rapports numériques inspirés par des motifs mathématiques.
• Formes musicales : Certains compositeurs ont exploré des formes musicales qui reflètent les propriétés de la suite de Fibonacci, créant des compositions qui évoluent de manière organique et naturelle.
• Utilisation de séquences numériques : Certains musiciens expérimentaux intègrent des séquences numériques, y compris la suite de Fibonacci, dans la création de motifs mélodiques et harmoniques. Ces séquences peuvent influencer la progression de la musique d'une manière qui évoque des motifs mathématiques.
Bien que la suite de Fibonacci ne soit pas un élément central de la composition musicale, elle peut servir d'inspiration pour des choix artistiques et structurels. Les musiciens qui s'intéressent aux relations entre les mathématiques et la musique peuvent incorporer des éléments de la suite de Fibonacci pour ajouter une dimension conceptuelle et intellectuelle à leur travail.
La suite de Fibonacci et la géométrie sacrée
Bien que la suite de Fibonacci ne soit pas intrinsèquement liée à la géométrie sacrée, ses propriétés mathématiques, en particulier le nombre d'or, ont été associées à des concepts de proportions harmonieuses et ont parfois été intégrées dans des interprétations de la géométrie sacrée.
Voici comment la suite de Fibonacci peut être liée à la géométrie sacrée :
• La Spirale d'Or : La spirale d'or, qui peut être dérivée de la suite de Fibonacci, est parfois considérée comme une forme géométrique sacrée. Cette spirale apparaît dans des motifs naturels tels que les coquilles d'escargot, les galaxies, et même dans certains motifs artistiques et architecturaux. Certains praticiens de la géométrie sacrée voient la spirale d'or comme un symbole de croissance, d'évolution et d'harmonie.
• Le Nombre d'Or (Phi) : Le nombre d'or, souvent noté par la lettre grecque phi (φ), est dérivé de la suite de Fibonacci. Il est défini comme la limite du rapport entre deux termes successifs de la suite à mesure que n tend vers l'infini. Le nombre d'or est considéré comme une proportion esthétiquement agréable et équilibrée, et il est associé à des concepts de beauté dans la géométrie sacrée.
• Proportions Harmonieuses : Les proportions dérivées de la suite de Fibonacci, en particulier le nombre d'or, sont parfois utilisées pour créer des formes géométriques dans des pratiques liées à la géométrie sacrée. Par exemple, la division d'un segment en utilisant le nombre d'or peut être vue comme une recherche de proportions équilibrées et significatives.
Exemples célèbres d'applications de la suite de Fibonacci
La suite de Fibonacci et ses propriétés mathématiques ont inspiré de nombreux artistes à travers les siècles. Voici quelques exemples célèbres de l'utilisation de la suite de Fibonacci dans l'art :
• La Naissance de Vénus - Sandro Botticelli : Cette célèbre peinture de la Renaissance italienne présente des proportions basées sur la suite de Fibonacci, en particulier dans la disposition des éléments du tableau. Les coquillages et les pétales de fleurs sur le sol suivent des motifs spiraloïdes qui rappellent la spirale d'or.
• La Joconde et l'Homme de Vitruve- Léonard de Vinci : Léonard de Vinci, qui était fasciné par les proportions harmonieuses, a utilisé la suite de Fibonacci dans certaines de ses œuvres, dont La Joconde. Certains estiment que la composition du visage de Mona Lisa suit des proportions basées sur la suite de Fibonacci.
• Le Parthénon - Phidias : Bien que le Parthénon ne date pas de l'époque de la suite de Fibonacci, l'architecte Phidias aurait utilisé des proportions basées sur la suite dans la conception du temple. Les colonnes et les dimensions du Parthénon reflètent des ratios qui évoquent la suite de Fibonacci et le fronton est inscrit dans un rectangle dont les dimensions des côtés adjacents ont le nombre d'or comme rapport.
• La spirale d'or dans l'œuvre de Salvador Dalí : Le célèbre peintre surréaliste Salvador Dalí a incorporé la spirale d'or, dérivée de la suite de Fibonacci, dans certaines de ses œuvres. Par exemple, "La Sacrament de la Dernière Cène" présente une spirale d'or qui guide le regard à travers la composition.
• Architecture de Le Corbusier : L'architecte Le Corbusier a appliqué les proportions de la suite de Fibonacci dans certaines de ses conceptions architecturales. Son utilisation de la proportion dorée peut être observée dans des bâtiments tels que la chapelle de Notre-Dame-du-Haut à Ronchamp.
• Musique de Béla Bartók et Iannis Xenakis : Bien que Béla Bartók ne se soit pas directement inspiré de la suite de Fibonacci, certains musicologues ont identifié des structures musicales dans ses compositions qui semblent refléter des motifs mathématiques similaires, évoquant l'idée de proportions harmonieuses. Le compositeur Iannis Xenakis a plusieurs fois utilisé la suite de Fibonacci : dès 1952 en tentant de créer une "image auditive" de cette série, puis dans quelques compositions : Zygia en 1952 et Le Sacrifice en 195353.
Ces exemples illustrent comment les artistes, qu'ils soient peintres, sculpteurs, architectes ou musiciens, ont exploré les principes de la suite de Fibonacci pour créer des œuvres esthétiquement plaisantes et harmonieuses. La fascination pour les motifs mathématiques dans l'art montre comment la beauté des proportions peut transcender les disciplines créatives.



Quel est l’intérêt de connaître la séquence de Fibonacci?
Si notre œil est attiré par la beauté, ce n’est pas un hasard !
Les Grecs anciens et les architectes de la Renaissance utilisèrent beaucoup phi pour établir les proportions des dimensions d’édifices qui nous émerveillent, et parfois même pour les proportions d'une simple porte ou fenêtre.
Il suffit d'observer certaines constructions pour comprendre que phi est plus qu'un simple concept arithmétique : il est à la racine de la beauté.
On retrouve la suite de Fibonacci dans la nature, et en fait, partout autour de nous (voir notre article sur le nombre d’or).
Les caractéristiques si particulières du nombre d'or ont captivé l'imagination d'innombrables mathématiciens, peintres, stylistes, biologistes, chimistes et même économistes. Ce nombre d'or est reflété dans certaines des plus grandes œuvres d'art et d'architecture créées au cours de l'histoire de l'humanité. Tout ne repose pas sur le nombre d'or, mais il apparaît dans une multitude vraiment stupéfiante d'endroits.
Et plus que tout, il touche notre perception de la beauté. Pour certains, cette beauté est centrée sur ses propriétés mathématiques et géométriques uniques ou sur sa capacité à créer un modèle fractal parfaitement formé. Pour d’autres il est perçu, consciemment ou non, dans la beauté de la nature, ainsi que dans le visage et le corps humain. Pour d'autres encore, intentionnellement ou non, il est exprimé dans leurs œuvres d'art et leurs conceptions créatives.
Et pour finir la question la plus importante que vous devez vous poser c'est comment et pourquoi vous percevez la beauté, pourquoi vous avez la capacité innée de voir la beauté et pourquoi vous avez aussi le besoin de l'exprimer.
Notre âme a simplement besoin de beauté pour être nourrie et se développer.
Tout comme notre corps a besoin de se nourrir d’aliments sains et équilibrés, notre âme, notre cœur, notre être véritable, a besoin de s’entourer d’objets harmonieux et lumineux.
Et c’est pour cette raison que nous avons développé tous les articles de géométrie sacrée que vous trouverez sur notre boutique en ligne !
Si vous avez aimé cet article, n’hésitez pas à commenter, à partager et à vous abonner à notre newsletter pour être informé(e) des prochaines parutions.
Inscrivez-vous à notre newsletter!
Sources:
Le nombre d’or aux Editions Dervy











 Étoile du sapin de Noël : la véritable signification
Étoile du sapin de Noël : la véritable signification
 Signification du Symbole Infini : un voyage vers l’éternité
Signification du Symbole Infini : un voyage vers l’éternité
 Symbolique du cercle : le mystère d’une forme parfaite
Symbolique du cercle : le mystère d’une forme parfaite
 Un esprit sain dans un corps sain : retrouver l’équilibre
Un esprit sain dans un corps sain : retrouver l’équilibre
 Mandala Fleur de Vie : un art de vivre au quotidien
Mandala Fleur de Vie : un art de vivre au quotidien
Ed Ma - 16/11/2024 20:22:51
Bonjour, Il est intéressant de noter que dans le poème « Genèse de l’Esprit » du poète polonais du XIXe siècle, Juliusz Słowacki (1809-1849), on peut lire : "La pensée mathématique elle-même semble s’être développée dans les plantes (Myśl, zda się, sama matematyczna rozwijała się w roślinach)" et "Chaque arbre est une grande solution à un problème mathématique, un mystère de nombre(s) (Każde drzewo jest wielkim rozwiązaniem matematycznego zadania, tajemnicą liczby)" Cordialement Ed Ma P.S. Cela peut aussi vous intéresser : "Big Bang" according to the 19th century polish poet J. Słowacki