La secuencia de Fibonacci

La secuencia de Fibonacci, llamada así por Leonardo Fibonacci, también conocido como Leonardo de Pisa, es una fascinante sucesión de números enteros que se ha abierto camino en diversos campos, desde las matemáticas hasta la arquitectura. Este matemático italiano del siglo XIII introdujo la secuencia de Fibonacci en su Liber Abaci, un manuscrito que ha sobrevivido al paso del tiempo para permitirnos ahondar en los misterios de esta particular secuencia. En la encrucijada de las matemáticas, el arte y la naturaleza, la secuencia de Fibonacci se ha convertido en una fuente inagotable de inspiración para muchos campos, ilustrando la presencia de motivos fascinantes como la espiral áurea y el crecimiento exponencial.
"No podemos comprender el universo si antes no nos esforzamos por entender su lenguaje y los caracteres con los que está escrito. Está escrito en lenguaje matemático"

¿Quién fue Leonardo Fibonacci?
Leonardo Fibonacci (c. 1175 en Pisa - c. 1250) fue un matemático italiano.
En aquella época, su nombre habitual era "Leonardo Pisano" (aún se le conoce en francés como Léonard de Pise), y a veces se hacía llamar "Leonardo Bigollo" (bigollo significa "viajero" en italiano).
Aunque se le conoce sobre todo por la secuencia de Fibonacci, su papel más importante fue servir de enlace entre los conocimientos matemáticos de los árabes, en particular los números indoárabes, y Occidente.
Su publicación más conocida es sin duda el Liber abaci (también escrito Liber abbaci), publicado en 1202.


El Libro de los cálculos es un tratado de cálculo y contabilidad basado en cálculos decimales en una época en la que todo Occidente seguía utilizando números romanos y cálculos con ábaco. El libro está fuertemente influenciado por su infancia en el Mediterráneo meridional y oriental, y está escrito en parte de derecha a izquierda.
Con esta publicación, Fibonacci introdujo en Europa el sistema de notación indoárabe importado de la India por las invasiones árabe-musulmanas. Este sistema era más potente y rápido que la notación romana, y Fibonacci era plenamente consciente de ello.
El invento no fue bien recibido al principio, ya que el público no entendía los cálculos que hacían los mercaderes. En 1280, Florencia llegó a prohibir el uso de números arábigos a los banqueros. Se consideró que el cero causaba tanta confusión y dificultad que llamaron al sistema cifra, que deriva del nombre árabe del cero (al sifr = vacío, cero). Gracias al uso de los números en la tradición cabalística, la palabra cifra adquirió el significado de código secreto.
Fibonacci es hoy más conocido por uno de sus problemas que dio lugar a los números y la secuencia que llevan su nombre, pero en su época fueron sobre todo las aplicaciones de la aritmética al cálculo comercial las que le hicieron famoso: cálculo del beneficio de las transacciones, conversión entre monedas de distintos países utilizando bases diferentes (base 10, 12, 20).
Su obra sobre la teoría de números fue ignorada en vida, pero fue muy leída durante los dos siglos siguientes. En la actualidad, su obra se utiliza ampliamente en las finanzas de mercado, sobre todo en el análisis técnico.
Definición de la secuencia de Fibonacci
La secuencia de Fibonacci, Fib, comienza con los dos primeros términos, 0 y 1, y cada término posterior es la suma de los dos términos precedentes, según la función Fib(n) = Fib(n-1) + Fib(n-2). La sucesión de Fibonacci también puede expresarse mediante la fórmula matemática, en la que el término de mayor índice n viene determinado por la siguiente relación. Estos primeros términos de la secuencia representan la pareja inicial de conejos, simbolizando el crecimiento de una población a lo largo de los meses.
Un ejemplo de aplicación factible de la secuencia de Fibonacci es modelizar el crecimiento de una población a lo largo de meses sucesivos, ilustrando una progresión que sigue una secuencia aritmética. La evolución de esta secuencia puede visualizarse en forma de cuarto de círculo, o incluso utilizarse para responder a cuestiones de divisibilidad o eficiencia en diversos problemas lúdicos. La secuencia de Fibonacci también tiene ramificaciones en campos como la arquitectura, donde la relación entre lados y longitudes laterales sigue una armonía matemática.
Leonardo de Pisa, autor de numerosos manuscritos, dejó un legado imborrable con la secuencia de Fibonacci, convirtiéndose en una clave de armonía en la modelización matemática en dinámica, un pequeño poema numérico que se despliega de punta a punta, y un modelo para figuras biológicas, como la concha del caracol. Todas las secuencias, incluido el triángulo de Pascal, se entrelazan con la de Fibonacci, demostrando la profundidad de sus relaciones en el vasto campo de las matemáticas.

¿Cuál es la ley de la secuencia de Fibonacci?
La secuencia de Fibonacci sigue una ley de recurrencia definida matemáticamente por la siguiente relación:
F(n)=F(n-1)+F(n-2)F(n)=F(n-1)+F(n-2)
con las condiciones iniciales F(0)=0F(0)=0 y F(1)=1F(1)=1. Esta relación expresa que cada término de la secuencia es la suma de los dos términos anteriores.
La fórmula explícita para calcular el enésimo término de la sucesión de Fibonacci sin necesidad de calcular todos los términos intermedios también se basa en una ley matemática, utilizando la proporción áurea (ϕ):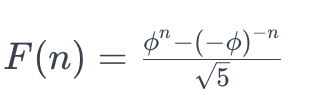
donde ϕ es la proporción áurea, aproximadamente igual a 1.618033988749895.
La secuencia de Fibonacci también tiene algunas propiedades interesantes relacionadas con la proporción áurea y la espiral áurea. Por ejemplo, a medida que nn se hace muy grande, la relación entre dos términos sucesivos de la secuencia de Fibonacci converge a la proporción áurea (ϕ).
En resumen, la ley fundamental de la secuencia de Fibonacci es la relación de recurrencia que define cada término en términos de los dos términos precedentes. Esta sencilla ley genera una secuencia de números con fascinantes propiedades matemáticas que tienen aplicaciones en diversos campos.
¿Cuál es el vínculo entre la proporción áurea y la secuencia de Fibonacci?
La relación entre la proporción áurea (o espiral áurea) y la secuencia de Fibonacci está estrechamente vinculada a la forma en que la sucesión de Fibonacci converge hacia la proporción áurea a medida que se avanza en los términos de la sucesión. La proporción áurea, a menudo representada por la letra griega φ (phi), es un valor irracional de aproximadamente 1,618033988749895. Este número tiene propiedades matemáticas únicas, y a menudo se asocia con proporciones estéticamente agradables en el arte, la arquitectura y la naturaleza.
El vínculo entre la proporción áurea y la secuencia de Fibonacci se ilustra mediante la siguiente relación: a medida que tomamos términos sucesivos de la secuencia de Fibonacci y dividimos cada término por su predecesor, el valor resultante converge a la proporción áurea. Formalmente, esto puede expresarse mediante el límite: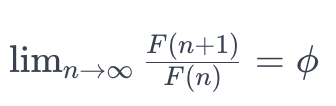
En esta ecuación, F(n)F(n) representa el enésimo término de la sucesión de Fibonacci. Esta propiedad de convergencia crea relaciones de longitud y patrones geométricos agradables que se observan a menudo en la naturaleza y se utilizan en el arte y la arquitectura. Por ejemplo, la espiral áurea, formada por la adición de cuadrados cuyos lados siguen la secuencia de Fibonacci, muestra un crecimiento basado en la proporción áurea, creando una espiral estéticamente agradable.
En resumen, el vínculo entre la sección áurea y la secuencia de Fibonacci reside en la convergencia de las relaciones entre los términos sucesivos de la secuencia hacia el valor de la sección áurea, dando lugar a patrones armoniosos y estéticos.
En la secuencia de Fibonacci, la relación de cada dos términos sucesivos converge hacia phi. Sin embargo, el matemático italiano nunca abordó específicamente la proporción áurea.
Para visualizar este fenómeno, observe que cada valor sucesivo de esta proporción se acerca cada vez más a phi:
1/1 = 1,000000
2/1 = 2,000000
3/2 = 1,500000
5/3 = 1,666667
8/5 = 1,600000
13/8 = 1,625000
21/13 = 1,615385
34/21 = 1,619048
55/34 = 1,617647
89/55 = 1,618182
144/89 = 1,617978
233/144 = 1,618056
377/233 = 1,618037
987/610 = 1,618033
De hecho, pasaron 400 años antes de que Johannes Kepler estableciera un vínculo explícito entre ambos. Fue el primero en mencionar claramente en una carta de 1609 que las proporciones de los términos sucesivos de la sucesión de Fibonacci se aproximan a la proporción áurea.
¿Cuál es el límite de la secuencia de Fibonacci?
La secuencia de Fibonacci no tiene límite finito, porque sus términos aumentan indefinidamente a medida que se avanza en la sucesión. Matemáticamente, esto se puede expresar diciendo que el límite de la sucesión de Fibonacci cuando n tiende a infinito no existe como número finito.
Formalmente, la definición de la secuencia de Fibonacci viene dada por la siguiente relación de recurrencia: F(n)=F(n-1)+F(n-2)F(n)=F(n-1)+F(n-2), con condiciones iniciales F(0)=0F(0)=0 y F(1)=1F(1)=1.
Si examinamos los términos de la secuencia, vemos que aumentan indefinidamente. Esto significa que, a medida que n se hace más y más grande, los valores de F(n)F(n) seguirán aumentando sin alcanzar un límite finito.
En notación matemática, esto se puede expresar como :
![]()
Esto indica que la secuencia de Fibonacci diverge hacia el infinito a medida que n tiende al infinito. Esta es una característica importante de la sucesión y refleja el crecimiento exponencial de los términos de la secuencia.
Secuencia matemática de Fibonacci: el ejemplo de los conejos
En su libro, Fibonacci también presenta una sencilla secuencia numérica basada en un problema teórico de multiplicación de una población de conejos. Esta secuencia, base de una increíble relación matemática subyacente a Phi, que los matemáticos indios ya conocían en el siglo VI, fue introducida en Occidente por Fibonacci.
La secuencia de Fibonacci puede explicarse con el siguiente ejemplo. Supongamos dos conejos recién nacidos, un macho y una hembra. Supongamos que los conejos son capaces de aparearse a la edad de 1 mes, de modo que al final de su segundo mes de vida la hembra producirá dos conejos. Supongamos que nuestros conejos nunca mueren y que la hembra produce dos conejos más (un macho y una hembra) cada mes, a partir de su segundo mes de vida.
Fibonacci se preguntó cuántos conejos tendríamos al cabo de un año. La respuesta es 144, que es el duodécimo número de la siguiente secuencia de crecimiento, correspondiente al duodécimo mes de nuevos conejos.

A partir de 0 y 1, cada nuevo término de la secuencia es simplemente la suma de los dos anteriores:
0 + 1 = 1
1 + 1 = 2
2 + 1 = 3
3 + 2 = 5
5 + 3 = 8
8 + 5 = 13
... etc., dando lugar a la siguiente secuencia, conocida como secuencia de Fibonacci:
0,1, 1, 2, 3, 5, 8, 13, 21,34, 55, 89, 144, 233, 377, 610, 987..
Espiral de Fibonacci
Si busca secuencias de Fibonacci en Internet, seguro que encuentra imágenes de espirales de Fibonacci o espirales de oro. También habrá visto esta espiral superpuesta en todo tipo de objetos, desde el Partenón a la Mona Lisa, pasando por el nacimiento del pelo de Donald Trump.
Normalmente, la espiral se crea tomando como base un rectángulo de oro. Divide el rectángulo dorado en su punta dorada y tendrás un cuadrado y otro rectángulo dorado más pequeño. Haz lo mismo una y otra vez con el rectángulo dorado más pequeño para crear la imagen de abajo.
Y dibujando un arco en cada cuadrado, obtendrás la espiral dorada.


Para una espiral relacionada, la espiral de Fibonacci, utilizamos cuadrados cuyas longitudes laterales son iguales a los términos de la secuencia de Fibonacci, en lugar de crear un patrón sucesivo de rectángulos áureos.
Técnicamente, no se trata de espirales, sino de volutas. La diferencia es casi imperceptible, pero una espiral verdadera es una espiral única, equiangular (en otras palabras, logarítmica) que se desarrolla a un ritmo constante. En la ilustración siguiente, la espiral verde está construida por una sucesión de arcos independientes en cada cuadrado. La espiral roja es una verdadera espiral logarítmica que incluye la sección áurea cada 90 grados (espiral equiangular). Las partes superpuestas están en amarillo.

¿Para qué se utiliza la secuencia de Fibonacci y cuándo? Aplicaciones.
La secuencia de Fibonacci es de gran importancia en diversos campos y se utiliza para una gran variedad de propósitos.
Estas son algunas de las aplicaciones y usos de la secuencia de Fibonacci:
- Modelización del crecimiento y de la población: La secuencia de Fibonacci puede utilizarse para modelizar el crecimiento de una población, especialmente en situaciones en las que cada generación depende de las anteriores.
- Análisis financiero: En el análisis técnico de los mercados financieros se utilizan aspectos de la secuencia de Fibonacci para identificar posibles niveles de soporte y resistencia.
- Arte y diseño: La espiral áurea, que está relacionada con la secuencia de Fibonacci, se utiliza en el arte y el diseño para crear proporciones estéticamente agradables. Artistas y arquitectos han incorporado estas proporciones en sus obras para crear armonía visual.
- Informática y algoritmos: La secuencia de Fibonacci se utiliza en informática, en particular para algoritmos recursivos y problemas de programación dinámica. La función fib se utiliza a menudo como ejemplo para enseñar la recursividad en informática.
- Criptografía: Algunos algoritmos criptográficos utilizan propiedades de la sucesión de Fibonacci para generar números aleatorios.
- Biología: Algunos modelos biológicos utilizan la sucesión de Fibonacci para describir el crecimiento de ciertas estructuras, como los pétalos de las flores o las conchas de los caracoles.
- Matemáticas puras: La sucesión de Fibonacci se estudia en matemáticas puras para comprender sus propiedades y comportamiento. También se utiliza para ilustrar diversos conceptos matemáticos a los estudiantes.
En resumen, la secuencia de Fibonacci no sólo tiene importancia matemática, sino que también tiene aplicaciones en muchos campos, desde el arte y la biología hasta las finanzas y la informática. Su ubicuidad demuestra la belleza y versatilidad de esta secuencia numérica.
La secuencia de Fibonacci en la naturaleza
La secuencia de Fibonacci se observa con frecuencia en la naturaleza, lo que ilustra cómo los patrones matemáticos pueden manifestarse en el mundo vivo. Varios ejemplos demuestran la presencia de esta secuencia en diversas estructuras biológicas, formas y fenómenos naturales. He aquí algunos ejemplos de la secuencia de Fibonacci en la naturaleza:
- Disposición de las hojas en un tallo: En muchas plantas, la disposición de las hojas en un tallo sigue la secuencia de Fibonacci. Por lo general, las hojas crecen de forma que maximicen la exposición a la luz solar y eviten la sombra de las hojas vecinas, creando una disposición en espiral que sigue la secuencia de Fibonacci.
- Espirales en las piñas: Las espirales que se encuentran en las piñas a menudo siguen la secuencia de Fibonacci. Las semillas se disponen en espiral para aprovechar al máximo el espacio y mantener al mismo tiempo una distribución uniforme.
- Conchas de caracoles y moluscos: Las conchas de algunos caracoles y moluscos siguen la forma de una espiral logarítmica, que está relacionada con la secuencia de Fibonacci. Esta estructura permite al animal crear una concha de forma eficiente, al tiempo que garantiza un crecimiento continuo.
- Flores y pétalos: El número de pétalos de muchas flores suele seguir secuencias de Fibonacci. Por ejemplo, las margaritas pueden tener 21, 34 o 55 pétalos, números que corresponden a términos sucesivos de la secuencia de Fibonacci.
- Ramificación de los árboles: La ramificación de las ramas de los árboles también puede seguir patrones basados en la secuencia de Fibonacci. Las ramas se dividen de manera que captan la luz solar con la máxima eficacia.
- Escamas de algunas frutas y verduras: la disposición de las escamas de algunas frutas, como la piña, sigue a veces la secuencia de Fibonacci, creando interesantes patrones geométricos.
La presencia de la secuencia de Fibonacci en estas estructuras naturales sugiere que esta secuencia numérica ofrece soluciones óptimas para los procesos de crecimiento y distribución en los reinos vegetal y animal. Es un testimonio de la belleza de las matemáticas en el diseño de la naturaleza.



La secuencia de Fibonacci en el arte y la arquitectura
La secuencia de Fibonacci y sus propiedades matemáticas también influyen en el campo del arte, donde se utiliza para crear obras estéticamente agradables y armoniosas. Los artistas han explorado la presencia de la secuencia de Fibonacci en diversas formas de arte, desde la pintura a la escultura, pasando por la arquitectura. He aquí algunas de las formas en que la secuencia de Fibonacci se expresa en el arte:
- Proporciones y cocientes: Las proporciones basadas en la secuencia de Fibonacci, en particular la proporción áurea, se utilizan a menudo para determinar el tamaño y la disposición de los elementos en una obra de arte. Estas proporciones se consideran estéticamente agradables y se han utilizado en famosas composiciones artísticas.
- Espirales áureas: La espiral áurea, derivada de la secuencia de Fibonacci, se utiliza para crear patrones en espiral en el arte. Los artistas han incorporado estas espirales en pinturas, esculturas y obras gráficas para crear una dinámica visual armoniosa.
- Mosaicos y azulejos: Algunos patrones de mosaicos y azulejos siguen las proporciones de la secuencia de Fibonacci. Estos patrones crean un efecto visual agradable y se utilizan en el arte decorativo, la arquitectura y el diseño de interiores.
- Frescos y murales: Los artistas utilizan la secuencia de Fibonacci para determinar el tamaño de los elementos en frescos y murales, creando composiciones equilibradas y estéticamente agradables.
- Fotografía y composición visual: Los fotógrafos a veces utilizan la secuencia de Fibonacci para componer imágenes de tal manera que llamen la atención y creen armonía visual. Las proporciones basadas en la secuencia de Fibonacci pueden aplicarse para guiar al espectador a través de una imagen.
- Arquitectura: Algunos arquitectos incorporan la secuencia de Fibonacci en el diseño de edificios y estructuras. Las proporciones basadas en la secuencia de Fibonacci pueden utilizarse para determinar la altura de los pisos, la anchura de las ventanas y otros elementos arquitectónicos.
El uso de la secuencia de Fibonacci en el arte demuestra cómo los conceptos matemáticos pueden inspirar la creación artística y contribuir a la percepción visual. Proporciona a los artistas un marco estructurado para expresar la belleza y la armonía en sus obras.

La secuencia de Fibonacci en la música
Aunque la secuencia de Fibonacci no se utiliza directamente en la composición musical del mismo modo que en las matemáticas, su influencia puede apreciarse en conceptos y estructuras armónicas. Músicos y compositores han explorado a veces ideas relacionadas con la secuencia de Fibonacci para crear patrones y estructuras en la música. He aquí algunas formas en que la secuencia de Fibonacci puede estar presente en la música:
- Ritmos y duraciones: Algunos compositores experimentan con patrones rítmicos basados en la secuencia de Fibonacci. Las duraciones de las notas pueden seguir secuencias que recuerdan la progresión de la secuencia, añadiendo una dimensión matemática a la estructura rítmica.
- Estructuras compositivas: Algunos músicos han utilizado los principios de la secuencia de Fibonacci para determinar la estructura de sus composiciones. Por ejemplo, la disposición de las secciones en una pieza musical puede seguir proporciones basadas en la secuencia de Fibonacci, creando una interesante progresión armónica y melódica.
- Frecuencias e intervalos: Las relaciones armónicas en la música, como las relaciones de intervalo entre notas, pueden estar influidas por conceptos matemáticos como la secuencia de Fibonacci. Aunque no siempre sea explícito, la búsqueda de consonancia y disonancia en la música puede estar vinculada a relaciones numéricas inspiradas en patrones matemáticos.
- Formas musicales: Algunos compositores han explorado formas musicales que reflejan las propiedades de la secuencia de Fibonacci, creando composiciones que evolucionan de forma orgánica y natural.
- Uso de secuencias numéricas: Algunos músicos experimentales incorporan secuencias numéricas, incluida la secuencia de Fibonacci, en la creación de patrones melódicos y armónicos. Estas secuencias pueden influir en la progresión de la música de un modo que evoca patrones matemáticos.
Aunque la secuencia de Fibonacci no es un elemento central de la composición musical, puede servir de inspiración para elecciones artísticas y estructurales. Los músicos interesados en la relación entre matemáticas y música pueden incorporar elementos de la secuencia de Fibonacci para añadir una dimensión conceptual e intelectual a su obra.
La secuencia de Fibonacci y la geometría sagrada
Aunque la secuencia de Fibonacci no está intrínsecamente vinculada a la geometría sagrada, sus propiedades matemáticas, en particular la proporción áurea, se han asociado a conceptos de proporciones armoniosas y a veces se han incorporado a interpretaciones de la geometría sagrada.
He aquí cómo la secuencia de Fibonacci puede vincularse a la geometría sagrada:
- La espiral áurea: La espiral áurea, que puede derivarse de la secuencia de Fibonacci, se considera a veces una forma geométrica sagrada. Esta espiral aparece en patrones naturales como las conchas de caracol y las galaxias, e incluso en ciertos motivos artísticos y arquitectónicos. Algunos practicantes de la geometría sagrada ven en la espiral áurea un símbolo de crecimiento, evolución y armonía.
- El número áureo (Phi): La proporción áurea, a menudo designada por la letra griega phi (φ), se deriva de la secuencia de Fibonacci. Se define como el límite de la relación entre dos términos sucesivos de la secuencia a medida que n tiende hacia el infinito. La proporción áurea se considera una proporción estéticamente agradable y equilibrada, y se asocia con conceptos de belleza en la geometría sagrada.
- Proporciones armoniosas: Las proporciones derivadas de la secuencia de Fibonacci, en particular la proporción áurea, se utilizan a veces para crear formas geométricas en prácticas relacionadas con la geometría sagrada. Por ejemplo, la división de un segmento utilizando la proporción áurea puede verse como una búsqueda de proporciones equilibradas y significativas.
Aplicaciones famosas de la secuencia de Fibonacci
La secuencia de Fibonacci y sus propiedades matemáticas han inspirado a muchos artistas a lo largo de los siglos. He aquí algunos ejemplos famosos del uso de la secuencia de Fibonacci en el arte:
- El nacimiento de Venus - Sandro Botticelli: Este famoso cuadro del Renacimiento italiano presenta proporciones basadas en la secuencia de Fibonacci, sobre todo en la disposición de los elementos del cuadro. Las conchas y los pétalos de las flores del fondo siguen patrones en espiral que recuerdan a la espiral áurea.
- La Gioconda y el Hombre de Vitruvio - Leonardo da Vinci: Leonardo da Vinci, fascinado por las proporciones armoniosas, utilizó la secuencia de Fibonacci en algunas de sus obras, entre ellas La Gioconda. Algunos creen que la composición del rostro de Mona Lisa sigue proporciones basadas en la secuencia de Fibonacci.
- El Partenón - Fidias: Aunque el Partenón no data de la época de la secuencia de Fibonacci, se dice que el arquitecto Fidias utilizó proporciones basadas en la secuencia al diseñar el templo. Las columnas y dimensiones del Partenón reflejan proporciones que evocan la secuencia de Fibonacci, y el frontón está inscrito en un rectángulo cuyos lados adyacentes tienen la proporción áurea.
- La espiral áurea en la obra de Salvador Dalí: El famoso pintor surrealista Salvador Dalí incorporó la espiral áurea, derivada de la secuencia de Fibonacci, en algunas de sus obras. Por ejemplo, "El sacramento de la última cena" presenta una espiral áurea que guía la mirada a través de la composición.
- Arquitectura de Le Corbusier: El arquitecto Le Corbusier aplicó las proporciones de la secuencia de Fibonacci en algunos de sus diseños arquitectónicos. Su uso de la proporción áurea puede verse en edificios como la capilla de Notre-Dame-du-Haut en Ronchamp.
- Música de Béla Bartók y Iannis Xenakis: Aunque Béla Bartók no se inspiró directamente en la secuencia de Fibonacci, algunos musicólogos han identificado estructuras musicales en sus composiciones que parecen reflejar patrones matemáticos similares, evocando la idea de proporciones armoniosas. El compositor Iannis Xenakis utilizó la secuencia de Fibonacci en varias ocasiones: ya en 1952, cuando intentó crear una "imagen auditiva" de esta serie, y después en varias composiciones: Zygia en 1952 y Le Sacrifice en 195353.
Estos ejemplos ilustran cómo los artistas, ya sean pintores, escultores, arquitectos o músicos, han explorado los principios de la secuencia de Fibonacci para crear obras estéticamente agradables y armoniosas. La fascinación por los patrones matemáticos en el arte muestra cómo la belleza de la proporción puede trascender las disciplinas creativas.



¿Para qué sirve conocer la secuencia de Fibonacci?
Si nuestros ojos se sienten atraídos por la belleza, ¡no es por casualidad!
Los antiguos griegos y los arquitectos del Renacimiento utilizaban mucho phi para establecer las proporciones de las dimensiones de edificios que nos asombran, y a veces incluso para las proporciones de una simple puerta o ventana.
Basta con observar algunos edificios para darse cuenta de que phi es algo más que un concepto aritmético: está en la raíz de la belleza.
La secuencia de Fibonacci se encuentra en la naturaleza y, de hecho, a nuestro alrededor (véase nuestro artículo sobre la proporción áurea).
Las características únicas de la proporción áurea han cautivado la imaginación de innumerables matemáticos, pintores, diseñadores, biólogos, químicos e incluso economistas. La proporción áurea se refleja en algunas de las mayores obras de arte y arquitectura creadas a lo largo de la historia de la humanidad. No todo se basa en la proporción áurea, pero aparece en una multitud de lugares realmente asombrosa.
Y, sobre todo, afecta a nuestra percepción de la belleza. Para algunos, esta belleza se centra en sus propiedades matemáticas y geométricas únicas o en su capacidad para crear un patrón fractal perfectamente formado. Para otros, se percibe, consciente o inconscientemente, en la belleza de la naturaleza, así como en el rostro y el cuerpo humanos. Para otros, intencionadamente o no, se expresa en sus obras de arte y diseños creativos.
Y por último, la pregunta más importante que debes hacerte es cómo y por qué percibes la belleza, por qué tienes la capacidad innata de verla y por qué tienes también la necesidad de expresarla.
Nuestra alma simplemente necesita la belleza para nutrirse y desarrollarse.
Al igual que nuestro cuerpo necesita nutrirse con alimentos sanos y equilibrados, nuestra alma, nuestro corazón, nuestro verdadero ser, necesita rodearse de objetos armoniosos y luminosos.
Y por eso hemos desarrollado todos los objetos de geometría sagrada que encontrarás en nuestra tienda online
Si te ha gustado este artículo, no dudes en comentarlo, compartirlo y suscribirte a nuestro boletín para estar informado de futuras ediciones.
¡Suscríbete a nuestro boletín!
Fuente:
Le nombre d'or publicado por Editions Dervy











 El Octágono: símbolo de justicia divina y equilibrio
El Octágono: símbolo de justicia divina y equilibrio
 Calendario de las 13 lunas: ¿un regreso a lo natural o un mito moderno?
Calendario de las 13 lunas: ¿un regreso a lo natural o un mito moderno?
 Simbolismo de la mariposa luna: metamorfosis interior
Simbolismo de la mariposa luna: metamorfosis interior
 ¿Qué colgante protector elegir?
¿Qué colgante protector elegir?
 Estrella del árbol de Navidad: el verdadero significado
Estrella del árbol de Navidad: el verdadero significado
Ed Ma - 16/11/2024 20:22:51
Bonjour, Il est intéressant de noter que dans le poème « Genèse de l’Esprit » du poète polonais du XIXe siècle, Juliusz Słowacki (1809-1849), on peut lire : "La pensée mathématique elle-même semble s’être développée dans les plantes (Myśl, zda się, sama matematyczna rozwijała się w roślinach)" et "Chaque arbre est une grande solution à un problème mathématique, un mystère de nombre(s) (Każde drzewo jest wielkim rozwiązaniem matematycznego zadania, tajemnicą liczby)" Cordialement Ed Ma P.S. Cela peut aussi vous intéresser : "Big Bang" according to the 19th century polish poet J. Słowacki