Die Fibonacci Folge

Die Fibonacci-Folge, benannt nach Leonardo Fibonacci, auch bekannt als Leonardo von Pisa, ist eine faszinierende Folge ganzer Zahlen, die in verschiedenen Bereichen von der Mathematik bis zur Architektur ihren Platz gefunden hat. Dieser italienische Mathematiker aus dem 13. Jahrhundert führte die Fibonacci-Folge in seinem Werk "Liber Abaci" ein, einem Manuskript, das die Zeit überdauert hat und es uns ermöglicht, in die Geheimnisse dieser besonderen Folge einzutauchen. An der Schnittstelle zwischen Mathematik, Kunst und Natur ist die Fibonacci-Folge zu einer unerschöpflichen Inspirationsquelle für viele Bereiche geworden und veranschaulicht die Präsenz faszinierender Muster wie der goldenen Spirale und des exponentiellen Wachstums.
"Man kann das Universum nicht verstehen, wenn man sich nicht zuerst darum bemüht, seine Sprache zu verstehen und die Schriftzeichen zu kennen, mit denen es geschrieben ist. Es ist in der Sprache der Mathematik geschrieben"

Wer ist Leonardo Fibonacci?
Leonardo Fibonacci (v. 1175 in Pisa - v. 1250) war ein italienischer Mathematiker.
Er hatte zu seiner Zeit den Gebrauchsnamen "Leonardo Pisano" (im Deutschen ist er noch heute unter dem Äquivalent Leonardo von Pisa bekannt) und nannte sich selbst manchmal "Leonardo Bigollo" (Bigollo bedeutet auf Italienisch "Reisender").
Er ist zwar für die Fibonacci-Folge bekannt, spielt aber vor allem eine Rolle von enormer Bedeutung, indem er das mathematische Wissen der Araber, insbesondere die indo-arabischen Zahlen, mit dem Westen verbindet.
Seine bekannteste Publikation ist sicherlich der Liber abaci (auch Liber abbaci geschrieben), der 1202 veröffentlicht wurde.


Das Buch der Berechnungen ist eine Abhandlung über das Rechnen und die Buchführung auf der Grundlage der Dezimalrechnung zu einer Zeit, als im gesamten Westen noch die römischen Zahlen verwendet und mit Abakus gerechnet wurde. Das Buch ist stark von seiner Kindheit beeinflusst, die er im südlichen und östlichen Mittelmeerraum verbracht hatte; es ist teilweise von rechts nach links verfasst.
Mit dieser Veröffentlichung führte Fibonacci das indo-arabische Notationssystem, das durch die arabisch-muslimischen Invasionen aus Indien importiert worden war, in Europa ein. Dieses System ist leistungsfähiger und schneller als die römische Notation, und Fibonacci ist sich dessen voll bewusst.
Die Erfindung wird zunächst schlecht aufgenommen, da die Öffentlichkeit die Berechnungen, die die Kaufleute anstellen, nicht mehr versteht. Im Jahr 1280 verbietet Florenz sogar die Verwendung arabischer Ziffern durch Bankiers. Man urteilt, dass die Null Verwirrung und Schwierigkeiten mit sich bringt, so dass sie das System cifra nennen, was vom arabischen Namen der Null (al sifr = leer, null) abgeleitet ist. Durch die Verwendung von Zahlen in der kabbalistischen Tradition soll das Wort Zahl die Bedeutung eines Geheimcodes erhalten haben.
Fibonacci ist heute eher für eines seiner Probleme bekannt, das zu den Zahlen und der nach ihm benannten Folge führt, aber zu seiner Zeit waren es vor allem die Anwendungen der Arithmetik auf die Handelsrechnung, die ihm Anerkennung einbrachten: Berechnung des Gewinns bei Transaktionen, Umrechnung von Währungen verschiedener Länder mit unterschiedlichen Basen (Basis 10, 12, 20).
Seine Arbeiten zur Zahlentheorie wurden zu seinen Lebzeiten ignoriert, in den folgenden zwei Jahrhunderten jedoch vielfach gelesen. Seine Arbeit wird heute vielfach in der Marktfinanzierung und insbesondere in der technischen Analyse verwendet.
Definition der Fibonacci-Folge
Die Fibonacci-Folge, auch Fib genannt, beginnt mit den ersten beiden Termen, 0 und 1, und jeder folgende Term ist die Summe der beiden vorhergehenden Terme, gemäß der Funktion Fib(n) = Fib(n-1) + Fib(n-2). Man kann die Fibonacci-Folge auch über die mathematische Formel ausdrücken, wobei der Term mit dem höchsten Index n durch die folgende Beziehung bestimmt wird. Diese ersten Terme der Folge stellen das anfängliche Kaninchenpaar dar und symbolisieren das Wachstum einer Population im Laufe der Monate.
Ein Beispiel für eine praktikable Anwendung der Fibonacci-Folge ist die Modellierung des Wachstums einer Population im Laufe aufeinanderfolgender Monate, die eine Progression nach einer arithmetischen Folge veranschaulicht. Die Entwicklung dieser Folge kann als Viertelkreis visualisiert werden oder sogar zur Beantwortung von Fragen zur Teilbarkeit oder Effizienz in verschiedenen Freizeitproblemen verwendet werden. Die Fibonacci-Folge verzweigt sich auch in Bereichen wie der Architektur, wo das Verhältnis zwischen Seiten und Seitenlängen einer mathematischen Harmonie folgt.
Leonardo da Pisa, der Autor zahlreicher Manuskripte, hinterließ mit der Fibonacci-Folge ein unauslöschliches Vermächtnis: Sie wurde zu einem Schlüssel zur Harmonie bei der mathematischen Modellierung in der Dynamik, zu einem kleinen numerischen Gedicht, das sich Ende zu Ende entfaltet, und zu einem Modell für biologische Figuren wie das Schneckenhaus. Alle Folgen, einschließlich des Pascalschen Dreiecks, sind mit der Fibonacci-Folge verwoben und demonstrieren die Tiefe ihrer Beziehungen im weiten Feld der Mathematik.

Was ist das Gesetz in der Fibonacci-Folge?
Die Fibonacci-Folge folgt einem Rekursionsgesetz, das mathematisch durch die folgende Beziehung definiert ist:
F(n)=F(n-1)+F(n-2)F(n)=F(n-1)+F(n-2)
mit den Anfangsbedingungen F(0)=0F(0)=0 und F(1)=1F(1)=1. Diese Beziehung drückt aus, dass jeder Term der Folge die Summe der beiden vorhergehenden Terme ist.
Die explizite Formel zur Berechnung des n-ten Terms der Fibonacci-Folge, ohne alle Zwischenterme berechnen zu müssen, basiert ebenfalls auf einem mathematischen Gesetz und verwendet den Goldenen Schnitt (ϕ):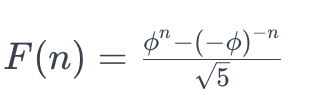
wobei ϕ der Goldene Schnitt ist, ungefähr gleich 1.618033988749895.
Die Fibonacci-Folge weist auch einige interessante Eigenschaften auf, die mit dem Goldenen Schnitt und der Goldenen Spirale zusammenhängen. Zum Beispiel konvergiert, je größer nn wird, das Verhältnis zwischen zwei aufeinanderfolgenden Termen der Fibonacci-Folge gegen den Goldenen Schnitt (ϕ).
Zusammenfassend lässt sich sagen, dass das grundlegende Gesetz in der Fibonacci-Folge die Rekursionsbeziehung ist, die jeden Term in Abhängigkeit von den beiden vorhergehenden Termen definiert. Dieses einfache Gesetz erzeugt eine Zahlenfolge, die faszinierende mathematische Eigenschaften aufweist und in verschiedenen Bereichen Anwendung findet.
Was ist die Verbindung zwischen dem Goldenen Schnitt und der Fibonacci-Folge?
Die Verbindung zwischen dem Goldenen Schnitt (oder der Goldenen Spirale) und der Fibonacci-Folge ist eng damit verknüpft, wie die Fibonacci-Folge gegen den Goldenen Schnitt konvergiert, je weiter man in den Termen der Folge fortschreitet. Der Goldene Schnitt, der oft durch den griechischen Buchstaben φ (phi) dargestellt wird, ist ein irrationaler Wert von etwa 1,618033988749895. Diese Zahl hat einzigartige mathematische Eigenschaften und wird in der Kunst, Architektur und Natur oft mit ästhetisch angenehmen Proportionen in Verbindung gebracht.
Die Verbindung zwischen dem Goldenen Schnitt und der Fibonacci-Folge wird durch folgende Beziehung veranschaulicht: Wenn man aufeinanderfolgende Terme der Fibonacci-Folge nimmt und jeden Term durch seinen Vorgänger teilt, konvergiert der resultierende Wert gegen den Goldenen Schnitt. Formal kann dies durch den Grenzwert ausgedrückt werden: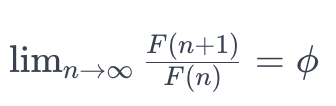
In dieser Gleichung stellt F(n)F(n) den n-ten Term der Fibonacci-Folge dar. Diese Konvergenzeigenschaft schafft angenehme Längenverhältnisse und geometrische Muster, die häufig in der Natur beobachtet und in der Kunst und Architektur verwendet werden. Die Goldene Spirale beispielsweise, die durch das Hinzufügen von Quadraten entsteht, deren Seiten der Fibonacci-Folge folgen, weist ein Wachstum auf, das auf dem Goldenen Schnitt basiert, und schafft eine ästhetisch ansprechende Spirale.
Zusammenfassend lässt sich sagen, dass die Verbindung zwischen dem Goldenen Schnitt und der Fibonacci-Folge darin besteht, dass das Verhältnis der aufeinanderfolgenden Terme der Folge zum Wert des Goldenen Schnitts konvergiert, was zu harmonischen und ästhetischen Mustern führt.
In der Fibonacci-Folge konvergiert das Verhältnis aller zwei aufeinanderfolgenden Terme zu phi. Dennoch hat sich der italienische Mathematiker nie speziell mit dem Goldenen Schnitt befasst.
Um dieses Phänomen zu veranschaulichen, stellen wir fest, dass jeder aufeinanderfolgende Wert dieses Verhältnisses sich phi immer mehr annähert:
1/1 = 1,00000000
2/1 = 2,00000000
3/2 = 1,500000
5/3 = 1,666667
8/5 = 1,600000
13/8 = 1,625000
21/13 = 1,615385
34/21 = 1,619048
55/34 = 1,617647
89/55 = 1,618182
144/89 = 1,617978
233/144 = 1,618056
377/233 = 1,618037
987/610 = 1,618033
Tatsächlich vergingen 400 Jahre, bevor Johannes Kepler eine explizite Verbindung zwischen den beiden herstellte. Er war der erste, der in einem Brief aus dem Jahr 1609 deutlich erwähnte, dass sich die Verhältnisse der aufeinanderfolgenden Terme der Fibonacci-Folge dem Goldenen Schnitt annähern.
Was ist der Grenzwert der Fibonacci-Folge?
Die Fibonacci-Folge hat keinen endlichen Grenzwert, da ihre Terme mit fortschreitender Folge unbegrenzt ansteigen. Mathematisch kann man dies so ausdrücken, dass der Grenzwert der Fibonacci-Folge, wenn n gegen unendlich geht, nicht als endliche Zahl existiert.
Formal ist die Definition der Fibonacci-Folge durch die folgende Rekursionsbeziehung gegeben: F(n)=F(n-1)+F(n-2)F(n)=F(n-1)+F(n-2), mit den Anfangsbedingungen F(0)=0F(0)=0 und F(1)=1F(1)=1.
Betrachtet man die Terme der Folge, so stellt man fest, dass sie unendlich ansteigen. Das bedeutet, dass mit zunehmend größer werdendem n die Werte von F(n)F(n) immer weiter ansteigen, ohne einen endlichen Grenzwert zu erreichen.
In mathematischer Notation kann man dies so ausdrücken, dass :
![]()
Dies deutet darauf hin, dass die Fibonacci-Folge gegen unendlich divergiert, wenn n gegen unendlich geht. Dies ist ein wichtiges Merkmal dieser Folge und spiegelt das exponentielle Wachstum der Terme der Folge wider.
Mathematische Fibonacci-Folge: Das Beispiel der Kaninchen
In seinem Buch stellt Fibonacci auch eine einfache Zahlenfolge vor, die auf einem theoretischen Problem der Vermehrung einer Kaninchenpopulation beruht. Diese Folge, die Grundlage einer unglaublichen mathematischen Beziehung unterhalb von Phi, die indische Mathematiker bereits im 6. Jahrhundert kannten, wurde von Fibonacci im Westen eingeführt.
Die Fibonacci-Folge lässt sich anhand des folgenden Beispiels erklären. Angenommen, es gibt zwei neugeborene Kaninchen, ein Männchen und ein Weibchen. Nehmen wir an, dass die Kaninchen im Alter von einem Monat paarungsfähig sind, dass also das Weibchen am Ende seines zweiten Lebensmonats zwei Kaninchen hervorbringen wird. Angenommen, unsere Kaninchen sterben nie und das Weibchen produziert ab ihrem zweiten Lebensmonat jeden Monat zwei weitere Kaninchen (ein Männchen, ein Weibchen).
Fibonacci fragte sich, wie viele Kaninchen wir am Ende in einem Jahr haben werden. Die Antwort lautet 144. Dies ist die 12. Zahl in der unten stehenden Wachstumsfolge, die dem 12. Monat mit neuen Kaninchen entspricht.

Ausgehend von 0 und 1 ist jeder neue Term der Folge einfach die Summe der beiden vorhergehenden Terme:
0 + 1 = 1
1 + 1 = 2
2 + 1 = 3
3 + 2 = 5
5 + 3 = 8
8 + 5 = 13
... usw., was zu der folgenden Folge führt, die den Namen Fibonacci trägt:
0,1, 1, 2, 3, 5, 8, 13, 21,34, 55, 89, 144, 233, 377, 610, 987..
Fibonacci-Spirale
Wenn Sie im Internet nach Fibonacci-Folgen suchen, stoßen Sie mit Sicherheit auf Bilder von Fibonacci-Spiralen oder Goldspiralen. Sie haben auch diese Spirale gesehen, die über alles gelegt wurde, vom Parthenon über Mona Lisa bis hin zu Donald Trumps Haaransatz.
Typischerweise wird die Spirale erstellt, indem man ein goldenes Rechteck als Basis nimmt. Teilen Sie das goldene Rechteck an seinem goldenen Punkt und Sie erhalten ein Quadrat und ein weiteres, kleineres goldenes Rechteck. Machen Sie das Gleiche immer wieder mit dem kleineren goldenen Rechteck, um das untenstehende Bild zu erzeugen.
Und indem man in jedes Quadrat einen Kreisbogen zeichnet, erhält man die goldene Spirale.


Für eine verwandte Spirale, die Fibonacci-Spirale, werden Quadrate verwendet, deren Seitenlänge den Termen der Fibonacci-Folge entspricht, anstatt ein aufeinanderfolgendes Muster aus goldenen Rechtecken zu schaffen.
Technisch gesehen handelt es sich nicht um Spiralen, sondern um Voluten. Der Unterschied ist praktisch nicht wahrnehmbar, aber eine echte ist eine einzelne, gleichseitige (d. h. logarithmische) Spirale, die sich in einem konstanten Tempo entwickelt. In der Abbildung unten wird die grüne Spirale durch eine Folge von unabhängigen Kreisbögen in jedem Quadrat aufgebaut. Die rote Spirale ist eine echte logarithmische Spirale, die alle 90 Grad den Goldenen Schnitt enthält (äquiangulare Spirale). Die sich überlagernden Teile sind gelb markiert.

Wozu dient die Fibonacci-Folge und wann wird sie verwendet? Die Anwendungen.
Die Fibonacci-Folge hat in verschiedenen Bereichen eine große Bedeutung und wird für unterschiedliche Zwecke verwendet.
Hier sind einige der Anwendungen und Verwendungen der Fibonacci-Folge:
- Modellierung von Wachstum und Bevölkerung: Die Fibonacci-Folge kann verwendet werden, um das Wachstum einer Bevölkerung zu modellieren, insbesondere in Situationen, in denen jede Generation von den vorherigen Generationen abhängt.
- Finanzanalyse: Einige Aspekte der Fibonacci-Folge werden in der technischen Analyse der Finanzmärkte verwendet, um potenzielle Unterstützungs- und Widerstandsniveaus zu identifizieren.
- Kunst und Design: Die goldene Spirale, die mit der Fibonacci-Folge in Verbindung steht, wird in der Kunst und im Design verwendet, um ästhetisch ansprechende Proportionen zu schaffen. Künstler und Architekten haben diese Proportionen in ihre Werke eingebaut, um eine visuelle Harmonie zu schaffen.
- Informatik und Algorithmen: Die Fibonacci-Folge wird im Bereich der Informatik verwendet, insbesondere für rekursive Algorithmen und dynamische Programmierprobleme. Die Funktion fib wird oft als Beispiel verwendet, um Rekursivität in der Informatik zu lehren.
- Kryptografie: Einige kryptografische Algorithmen nutzen Eigenschaften der Fibonacci-Folge, um Zufallszahlen zu erzeugen.
- Biologie: Einige biologische Modelle stützen sich auf die Fibonacci-Folge, um das Wachstum bestimmter Strukturen, wie Blütenblätter oder Schneckenhäuser, zu beschreiben.
- Reine Mathematik: Die Fibonacci-Folge wird in der reinen Mathematik untersucht, um ihre Eigenschaften und ihr Verhalten zu verstehen. Sie wird auch verwendet, um Schülern verschiedene mathematische Konzepte zu veranschaulichen.
Zusammenfassend lässt sich sagen, dass die Fibonacci-Folge nicht nur eine mathematische Bedeutung hat, sondern in vielen Bereichen Anwendung findet, von der Kunst über die Biologie bis hin zum Finanzwesen und der Informatik. Ihre Allgegenwärtigkeit zeigt die Schönheit und Vielseitigkeit dieser Zahlenfolge.
Die Fibonacci-Folge in der Natur
Die Fibonacci-Folge ist in der Natur häufig zu beobachten und veranschaulicht, wie sich mathematische Modelle in der lebenden Welt manifestieren können. Mehrere Beispiele zeigen, dass diese Folge in verschiedenen biologischen Strukturen, Formen und Naturphänomenen vorkommt. Hier einige Beispiele für die Fibonacci-Folge in der Natur:
- Anordnung der Blätter an einem Stängel: Bei vielen Pflanzen folgt die Anordnung der Blätter an einem Stängel der Fibonacci-Folge. Die Blätter wachsen in der Regel so, dass sie möglichst viel Sonnenlicht abbekommen und den Schatten benachbarter Blätter vermeiden, wodurch eine spiralförmige Anordnung entsteht, die der Fibonacci-Folge entspricht.
- Spiralen in Tannenzapfen: Die auf Tannenzapfen vorhandenen Spiralen folgen oft der Fibonacci-Folge. Die Samen werden in Spiralen angeordnet, um den Platz zu maximieren und gleichzeitig eine gleichmäßige Verteilung zu erhalten.
- Schnecken- und Muschelschalen: Die Schalen einiger Schnecken und Muscheln folgen der Form einer logarithmischen Spirale, die mit der Fibonacci-Folge verbunden ist. Diese Struktur ermöglicht es dem Tier, eine Schale effizient zu schaffen und gleichzeitig ein kontinuierliches Wachstum zu gewährleisten.
- Blumen und Blütenblätter: Die Anzahl der Blütenblätter in vielen Blumen folgt oft Fibonacci-Folgen. Margeriten können z. B. 21, 34 oder 55 Blütenblätter haben, Zahlen, die aufeinanderfolgenden Termen der Fibonacci-Folge entsprechen.
- Baumverzweigung: Die Verzweigung der Äste von Bäumen kann ebenfalls Mustern folgen, die auf der Fibonacci-Folge basieren. Die Äste teilen sich so, dass die Effizienz beim Einfangen des Sonnenlichts maximiert wird.
- Schuppen einiger Obst- und Gemüsesorten: Die Anordnung der Schuppen auf einigen Früchten, wie z. B. der Ananas, folgt manchmal der Fibonacci-Folge, wodurch interessante geometrische Muster entstehen.
Das Vorhandensein der Fibonacci-Folge in diesen natürlichen Strukturen legt nahe, dass diese Zahlenfolge optimale Lösungen für Wachstums- und Verteilungsprozesse im Pflanzen- und Tierreich bietet. Dies zeugt von der Schönheit der Mathematik bei der Gestaltung der Natur.



Die Fibonacci-Folge in Kunst und Architektur
Die Fibonacci-Folge und ihre mathematischen Eigenschaften beeinflussen auch den künstlerischen Bereich, wo sie dazu verwendet wird, ästhetisch ansprechende und harmonische Werke zu schaffen. Künstler haben die Präsenz der Fibonacci-Folge in verschiedenen Kunstformen erforscht, von der Malerei über die Architektur bis hin zu Skulpturen. Hier sind einige Möglichkeiten, wie sich die Fibonacci-Folge in der Kunst ausdrückt:
- Proportionen und Verhältnisse: Proportionen, die auf der Fibonacci-Folge basieren, insbesondere der Goldene Schnitt, werden häufig verwendet, um die Größe und Anordnung von Elementen in einem Kunstwerk zu bestimmen. Diese Verhältnisse gelten als ästhetisch ansprechend und wurden in berühmten künstlerischen Kompositionen verwendet.
- Goldene Spiralen: Die goldene Spirale, die sich aus der Fibonacci-Folge ableitet, wird bei der Schaffung von Spiralmustern in der Kunst verwendet. Künstler haben diese Spiralen in Gemälde, Skulpturen und Grafiken eingearbeitet, um eine harmonische visuelle Dynamik zu erzeugen.
- Mosaike und Fliesen: Einige Muster in Mosaiken und Fliesen folgen den Proportionen der Fibonacci-Folge. Diese Muster erzeugen einen angenehmen visuellen Effekt und werden in der dekorativen Kunst, Architektur und Innenarchitektur verwendet.
- Fresken und Wandmalereien: Künstler verwenden die Fibonacci-Folge, um die Größe der Elemente in Fresken und Wandmalereien zu bestimmen, und schaffen so ausgewogene und ästhetisch befriedigende Kompositionen.
- Fotografie und visuelle Komposition: Fotografen verwenden manchmal die Fibonacci-Folge, um Bilder so zu komponieren, dass sie das Auge anziehen und eine visuelle Harmonie schaffen. Proportionen, die auf der Fibonacci-Folge basieren, können angewendet werden, um den Betrachter durch ein Bild zu führen.
- Architektur: Einige Architekten integrieren die Fibonacci-Folge in die Gestaltung von Gebäuden und Strukturen. Proportionen, die auf der Fibonacci-Folge basieren, können verwendet werden, um die Höhe von Stockwerken, die Breite von Fenstern und andere architektonische Elemente zu bestimmen.
Die Verwendung der Fibonacci-Folge in der Kunst zeigt, wie mathematische Konzepte das künstlerische Schaffen inspirieren und zur visuellen Wahrnehmung beitragen können. Dies bietet Künstlern einen strukturierten Rahmen, um Schönheit und Harmonie in ihren Werken auszudrücken.

Die Fibonacci-Folge in der Musik
Obwohl die Fibonacci-Folge in der Musikkomposition nicht direkt in der gleichen Weise wie in der Mathematik verwendet wird, zeigt sich ihr Einfluss in harmonischen Konzepten und Strukturen. Musiker und Komponisten haben manchmal Ideen im Zusammenhang mit der Fibonacci-Folge erforscht, um Muster und Strukturen in der Musik zu schaffen. Hier sind einige Möglichkeiten, wie die Fibonacci-Folge in der Musik vorkommen kann:
- Rhythmen und Dauern: Einige Komponisten experimentieren mit rhythmischen Mustern, die auf der Fibonacci-Folge basieren. Die Dauern der Noten können Sequenzen folgen, die an die Progression der Folge erinnern und der rhythmischen Struktur eine mathematische Dimension hinzufügen.
- Kompositionsstrukturen: Einige Musiker haben die Prinzipien der Fibonacci-Folge verwendet, um die Struktur ihrer Kompositionen zu bestimmen. Beispielsweise kann die Anordnung der Abschnitte eines Musikstücks Proportionen folgen, die auf der Fibonacci-Folge basieren, und so eine interessante harmonische und melodische Progression schaffen.
- Frequenzen und Intervalle: Harmonische Beziehungen in der Musik, wie etwa die Intervallverhältnisse zwischen Noten, können von mathematischen Konzepten wie der Fibonacci-Folge beeinflusst werden. Obwohl es vielleicht nicht immer explizit ist, kann die Suche nach Konsonanz und Dissonanz in der Musik mit Zahlenverhältnissen verbunden sein, die von mathematischen Mustern inspiriert sind.
- Musikalische Formen: Einige Komponisten haben musikalische Formen erforscht, die die Eigenschaften der Fibonacci-Folge widerspiegeln, und Kompositionen geschaffen, die sich organisch und natürlich entwickeln.
- Verwendung digitaler Sequenzen: Einige experimentelle Musiker integrieren digitale Sequenzen, einschließlich der Fibonacci-Folge, in die Schaffung von melodischen und harmonischen Mustern. Diese Sequenzen können den Verlauf der Musik auf eine Weise beeinflussen, die an mathematische Muster erinnert.
Obwohl die Fibonacci-Folge kein zentrales Element der musikalischen Komposition ist, kann sie als Inspiration für künstlerische und strukturelle Entscheidungen dienen. Musiker, die sich für die Beziehung zwischen Mathematik und Musik interessieren, können Elemente der Fibonacci-Folge einbauen, um ihrer Arbeit eine konzeptionelle und intellektuelle Dimension zu verleihen.
Die Fibonacci-Folge und die heilige Geometrie
Obwohl die Fibonacci-Folge nicht von Natur aus mit der heiligen Geometrie verbunden ist, wurden ihre mathematischen Eigenschaften, insbesondere der Goldene Schnitt, mit Konzepten harmonischer Proportionen in Verbindung gebracht und manchmal in Interpretationen der heiligen Geometrie integriert.
So kann die Fibonacci-Folge mit der heiligen Geometrie in Verbindung gebracht werden:
- Die Goldene Spirale: Die goldene Spirale, die von der Fibonacci-Folge abgeleitet werden kann, wird manchmal als eine heilige geometrische Form betrachtet. Diese Spirale erscheint in natürlichen Mustern wie Schneckenhäusern, Galaxien und sogar in einigen künstlerischen und architektonischen Mustern. Einige Praktiker der heiligen Geometrie sehen die goldene Spirale als ein Symbol für Wachstum, Evolution und Harmonie.
- Der Goldene Schnitt (Phi): Der Goldene Schnitt, oft mit dem griechischen Buchstaben Phi (φ) notiert, ist von der Fibonacci-Folge abgeleitet. Er ist definiert als der Grenzwert des Verhältnisses zwischen zwei aufeinanderfolgenden Termen der Folge, je weiter n gegen unendlich geht. Der Goldene Schnitt gilt als ästhetisch ansprechende und ausgewogene Proportion und wird in der heiligen Geometrie mit Konzepten der Schönheit in Verbindung gebracht.
- Harmonische Proportionen: Die aus der Fibonacci-Folge abgeleiteten Proportionen, insbesondere der Goldene Schnitt, werden in Praktiken, die mit der heiligen Geometrie in Verbindung stehen, manchmal zur Schaffung geometrischer Formen verwendet. Beispielsweise kann die Teilung eines Segments unter Verwendung des Goldenen Schnitts als Suche nach ausgewogenen und bedeutungsvollen Proportionen gesehen werden.
Berühmte Beispiele für die Anwendung der Fibonacci-Folge
Die Fibonacci-Folge und ihre mathematischen Eigenschaften haben im Laufe der Jahrhunderte viele Künstler inspiriert. Hier sind einige berühmte Beispiele für die Anwendung der Fibonacci-Folge in der Kunst:
- Die Geburt der Venus - Sandro Botticelli: Dieses berühmte Gemälde aus der italienischen Renaissance zeigt Proportionen, die auf der Fibonacci-Folge basieren, insbesondere bei der Anordnung der Elemente des Bildes. Die Muscheln und Blütenblätter auf dem Boden folgen spiralförmigen Mustern, die an die goldene Spirale erinnern.
- Die Mona Lisa und der vitruvianische Mensch- Leonardo da Vinci: Leonardo da Vinci, der von harmonischen Proportionen fasziniert war, verwendete die Fibonacci-Folge in einigen seiner Werke, darunter auch in der Mona Lisa. Manche glauben, dass die Komposition des Gesichts von Mona Lisa Proportionen folgt, die auf der Fibonacci-Folge basieren.
- Der Parthenon - Phidias: Obwohl der Parthenon nicht aus der Zeit der Fibonacci-Folge stammt, soll der Architekt Phidias bei der Gestaltung des Tempels Proportionen verwendet haben, die auf der Folge basieren. Die Säulen und Abmessungen des Parthenon spiegeln Verhältnisse wider, die an die Fibonacci-Folge erinnern, und der Giebel ist in ein Rechteck einbeschrieben, dessen Abmessungen der angrenzenden Seiten den Goldenen Schnitt als Verhältnis haben.
- Die Goldene Spirale in den Werkenvon Salvador Dalí: Der berühmte surrealistische Maler Salvador Dalí hat die Goldene Spirale, die von der Fibonacci-Folge abgeleitet ist, in einige seiner Werke eingebaut. Zum Beispiel weist "Das Sakrament des letzten Abendmahls" eine goldene Spirale auf, die den Blick durch die Komposition leitet.
- Architektur von Le Corbusier: Der Architekt Le Corbusier hat die Proportionen der Fibonacci-Folge in einigen seiner architektonischen Entwürfe angewandt. Seine Verwendung des goldenen Schnitts kann in Gebäuden wie der Kapelle Notre-Dame-du-Haut in Ronchamp beobachtet werden.
- Musik von Béla Bartók und Iannis Xenakis: Obwohl Béla Bartók sich nicht direkt von der Fibonacci-Folge inspirieren ließ, haben einige Musikwissenschaftler musikalische Strukturen in seinen Kompositionen identifiziert, die ähnliche mathematische Muster widerzuspiegeln scheinen und die Idee harmonischer Proportionen heraufbeschwören. Der Komponist Iannis Xenakis hat die Fibonacci-Folge mehrfach verwendet: bereits 1952 bei dem Versuch, ein "Hörbild" dieser Reihe zu schaffen, und dann in einigen Kompositionen: Zygia 1952 und Le Sacrifice 195353.
Diese Beispiele zeigen, wie Künstler, ob Maler, Bildhauer, Architekten oder Musiker, die Prinzipien der Fibonacci-Folge erforscht haben, um ästhetisch ansprechende und harmonische Werke zu schaffen. Die Faszination für mathematische Muster in der Kunst zeigt, wie die Schönheit der Proportionen über kreative Disziplinen hinausgehen kann.



Warum ist es wichtig, die Fibonacci-Folge zu kennen?
Es ist kein Zufall, dass unser Auge von Schönheit angezogen wird!
Die alten Griechen und die Architekten der Renaissance verwendeten phi häufig, um die Proportionen von Gebäuden zu bestimmen, die uns in Staunen versetzen, und manchmal sogar für die Proportionen einer einfachen Tür oder eines Fensters.
Man muss sich nur einige Bauwerke ansehen, um zu verstehen, dass phi mehr als nur ein arithmetisches Konzept ist: Es ist die Wurzel der Schönheit.
Die Fibonacci-Folge findet man in der Natur und eigentlich überall um uns herum (siehe unseren Artikel über den Goldenen Schnitt).
Die so besonderen Eigenschaften des Goldenen Schnitts haben die Fantasie unzähliger Mathematiker, Maler, Modedesigner, Biologen, Chemiker und sogar Wirtschaftswissenschaftler gefesselt. Der Goldene Schnitt spiegelt sich in einigen der größten Kunstwerke und Architekturen wider, die in der Geschichte der Menschheit geschaffen wurden. Nicht alles beruht auf dem Goldenen Schnitt, aber er taucht an einer wirklich verblüffenden Vielzahl von Orten auf.
Und mehr als alles andere berührt er unsere Wahrnehmung von Schönheit. Für manche konzentriert sich diese Schönheit auf seine einzigartigen mathematischen und geometrischen Eigenschaften oder auf seine Fähigkeit, ein perfekt geformtes fraktales Muster zu schaffen. Für andere wird sie, bewusst oder unbewusst, in der Schönheit der Natur sowie im menschlichen Gesicht und Körper wahrgenommen. Für wieder andere kommt es absichtlich oder unabsichtlich in ihren Kunstwerken und kreativen Entwürfen zum Ausdruck.
Und schließlich ist die wichtigste Frage, die Sie sich stellen müssen, wie und warum Sie Schönheit wahrnehmen, warum Sie die angeborene Fähigkeit haben, Schönheit zu sehen, und warum Sie auch das Bedürfnis haben, sie auszudrücken.
Unsere Seele braucht Schönheit einfach, um genährt zu werden und sich zu entwickeln.
So wie unser Körper sich von gesunder und ausgewogener Nahrung ernähren muss, muss sich unsere Seele, unser Herz, unser wahres Wesen mit harmonischen und leuchtenden Objekten umgeben.
Und aus diesem Grund haben wir alle Artikel zur Heiligen Geometrie entwickelt, die Sie in unserem Online-Shop finden!
Wenn Ihnen dieser Artikel gefallen hat, kommentieren Sie ihn, teilen Sie ihn mit anderen und abonnieren Sie unseren Newsletter, um über zukünftige Veröffentlichungen informiert zu werden.
Melden Sie sich für unseren Newsletter an!
Quellen:
Le nombre d'or (Der goldene Schnitt), Editions Dervy











 Das Achteck: Symbol göttlicher Gerechtigkeit und Balance
Das Achteck: Symbol göttlicher Gerechtigkeit und Balance
 13-Monde-Kalender: Rückkehr zur Natur oder moderner Mythos?
13-Monde-Kalender: Rückkehr zur Natur oder moderner Mythos?
 Symbolik des Mondfalters: eine innere Metamorphose
Symbolik des Mondfalters: eine innere Metamorphose
 Welchen Schutzanhänger sollten Sie wählen?
Welchen Schutzanhänger sollten Sie wählen?
 Stern auf dem Weihnachtsbaum: die wahre Bedeutung
Stern auf dem Weihnachtsbaum: die wahre Bedeutung
Ed Ma - 16.11.2024 20:22:51
Bonjour, Il est intéressant de noter que dans le poème « Genèse de l’Esprit » du poète polonais du XIXe siècle, Juliusz Słowacki (1809-1849), on peut lire : "La pensée mathématique elle-même semble s’être développée dans les plantes (Myśl, zda się, sama matematyczna rozwijała się w roślinach)" et "Chaque arbre est une grande solution à un problème mathématique, un mystère de nombre(s) (Każde drzewo jest wielkim rozwiązaniem matematycznego zadania, tajemnicą liczby)" Cordialement Ed Ma P.S. Cela peut aussi vous intéresser : "Big Bang" according to the 19th century polish poet J. Słowacki