Sólidos platónicos: símbolos de perfección

Los Sólidos Platónicos provienen de la Geometría Sagrada, una tradición pitagórica transmitida a Platón durante su enseñanza en la Academia, donde estudió bajo la tutela de su mentor, Espeusipo. Platón, sucesor de Sócrates, profundizó este conocimiento matemático y filosófico, cuyos fundamentos se remontan a la antigua Grecia y a matemáticos como Teeteto de Atenas.
Estos sólidos, también conocidos como poliedros regulares convexos, tienen propiedades notables. Todos ellos pueden inscribirse en esferas y sus caras, aristas y ángulos son iguales. Esta regularidad los hace particularmente significativos en la representación de formas y estructuras del universo.
Entre los sólidos, dos de ellos, el dodecaedro y el icosaedro, no se describen en los primeros escritos de Platón. Por otro lado, se atribuyen a Arquitas de Tarento, matemático y filósofo griego contemporáneo de Platón.
Los matemáticos griegos estudiaron en profundidad estas formas. Esto les permitió descubrir relaciones importantes entre ellos, como la suma de los ángulos de las caras y la fórmula de Euler. Es más, estos sólidos están vinculados a la noción de proporción áurea, la proporción matemática que se considera estéticamente armoniosa.
Cada forma tiene propiedades muy interesantes que te invito a descubrir en este artículo.
¿Vamos?

¿Quién inventó los sólidos platónicos?
Los sólidos platónicos no son estrictamente "inventados" por el propio Platón. Fueron descubiertos y estudiados por los matemáticos griegos mucho antes de la época de Platón, pero Platón los hizo famosos en sus diálogos filosóficos, especialmente en su obra llamada "Timeo".
Los Sólidos llevan el nombre de Platón porque fue él quien los describió y los hizo populares en sus escritos. Sin embargo, parecería que su estudio se remonta mucho antes de Platón, en la época griega de Pitágoras y sus discípulos.
Qué son los sólidos platonicos ¿Por qué 5 sólidos de Platón?
Los sólidos juegan un papel determinante en la filosofía de Platón. El filósofo griego, en el diálogo Timeo (c. 358 a. C.), asoció cada uno de los cuatro elementos (tierra, aire, agua y fuego) a un sólido regular. Estos cinco sólidos tienen la particularidad de ser polígonos regulares, es decir figuras con varias caras que pueden encajar en un círculo y todos cuyos vértices (esquinas) están en contacto con el círculo.
Nombre, naturaleza y virtudes de los sólidos platónicos
Platón consideró que estos polígonos tridimensionales eran perfectos y dio la definición de cinco de ellos:
| Elemento | Sólido platónico | Número de aristas | Número de planes | Número de caras | Número de vértices | Forma de cada cara |
| Éter | Dodecaedro | 30 | 60 | 12 | 20 | Pentágono |
| Fuego | Tetraedro | 6 | 12 | 4 | 4 | Triángulo |
| Aire | Octaedro | 12 | 24 | 8 | 6 | Triángulo |
| Agua | Icosaedro | 30 | 60 | 20 | 12 | Triángulo |
| Tierra | Hexaedro (cubo) | 12 | 24 | 6 | 8 | Cuadrado |




Estos cinco sólidos ocuparon un lugar importante en la geometría práctica, pero también en la mística, aunque Platón no fue el primero en considerarlos: los tres primeros pertenecen a Pitágoras y los dos últimos a Teeteto (en el siglo IV a.C.).
Millones de formas están formadas por polígonos irregulares, pero sólo cinco sólidos están formados por polígonos regulares.
Esta singularidad llevó a Aristóteles y Platón a considerar que estas figuras eran la base de la materia y las asociaron a los cuatro elementos a los que añadieron el éter (Aether en latín).
Edra significa simplemente superficie, por lo que los poliedros regulares son formas 3D compuestas por superficies que son figuras simétricas con varias caras.
Es posible relacionar todas estas figuras entre sí mediante la fórmula maestra: número de aristas + 2 = número de caras + número de vértices.
Aunque estos sólidos parecen complejos, en realidad son bastante sencillos.
- El cubo es la más básica y regular de las formas de caja.
- El tetraedro es una pirámide con base triangular.
- El octaedro está formado por dos pirámides idénticas de base cuadrada, que se unen entre sí.
Cada sólido tiene una virtud, una influencia propia, como los símbolos de la geometría sagrada.
El tetraedro, vinculado al fuego, es un elemento activo, cuyo simbolismo está ligado a la aparición de la elevación.
La vibración de la forma del tetraedro puede fortalecer nuestra salud en general o puede amplificar una intención. El uso del tetraedro puede ayudarnos a superar una fatiga importante o a activar una convalecencia.
El hexaedro, conectado a la tierra, es un elemento de danza estable y la vibración de su forma favorecerá la estabilidad, la precisión y la seguridad. Favorecerá una buena gestión del mundo material y, por tanto, la supervivencia del cuerpo físico.
El octaedro, vinculado al aire, es un elemento muy sutil, cuyo simbolismo es el intercambio entre todas las direcciones y todas las dimensiones. Promueve la sutileza y la ligereza para nuestro entorno psíquico. También ayuda a fortalecer el aura.
El icosaedro, vinculado al agua, es un elemento que favorece la fluidez, la disolución y la pureza. Puede ayudar a abrir el chakra del corazón y nos conecta con nuestra alma causal. Es muy adecuado para ayudarnos a disolver nuestros bloqueos para crear una emisión de afecto y amor hacia los demás, para cambiar nuestra emisión vibratoria y para cambiar nuestra vida.
El dodecaedro, vinculado al éter, simboliza el quinto elemento, la energía invisible que subyace a los cuatro elementos formales. Promueve nuestro desarrollo espiritual y una conexión con nuestra alma espiritual y nuestro programa de encarnación.
Los sólidos platónicos y los elementos
Los cinco sólidos forman dos grupos de elementos: los duales, por un lado, y el éter, por otro. El cubo (tierra) y el octaedro (aire) son geométricamente duales, es decir, uno puede crearse dentro del otro conectando los puntos que marcan el centro de cada cara. Así, un cubo puede convertirse en un octaedro, y viceversa, ad infinitum.
Asimismo, los otros dos elementos representados por el tetraedro (fuego) y el icosaedro (agua) son duales y pueden generarse mutuamente.
Por tanto, existe una simetría perfecta entre cada par de elementos, tierra-aire y agua-fuego. El dodecaedro es dual en sí mismo, por lo que el éter puede generarse a sí mismo.
Así que, si resumimos un poco
Platón relaciona los sólidos con las grandes entidades que, según él, daban forma al mundo: el fuego, el aire, el agua, la tierra y el éter.
Cada uno está vinculado a un elemento de la Creación:
- 1º Sólido platónico: el Tetraedro: el fuego
- 2º Sólido platónico: el Octaedro: el aire
- 3º Sólido dplatónico: el Icosaedro: el agua
- 4º Sólido platónico: el Cubo: la tierra
- 5º Sólido platónico: el Dodecaedro: representa el Todo, el Universo
La esfera sólida
La esfera es realmente el volumen perfecto en el que cada punto de la superficie está a igual distancia del centro y en el que todas las presiones ejercidas sobre su superficie están en equilibrio, lo que le da su forma (como una gota de líquido en ingravidez).
Somos un 70-80% de agua y este elemento está simbolizado por la esfera, la gota, el lago, las olas, nos habla internamente.
La visión de una esfera nos pone inmediatamente en resonancia con nuestro planeta, los cuerpos celestes, las estrellas y el cosmos. El sol y la luna han sido deificados durante miles de años. Así, han quedado como símbolos de perfección en el inconsciente colectivo.
La esfera irradia y armoniza el espacio que la rodea a una distancia proporcional a su tamaño. El uso de una esfera de cristal como rearmonizador es muy común en el Feng Shui y la geobiología. Es una buena herramienta para restablecer una tasa vibratoria global satisfactoria.
Eche un vistazo a nuestra colección de cristales captador de sol.
La bola de cristal es bien conocida por su uso en la clarividencia y la mediumnidad, pero también es una buena herramienta para la meditación.

Los sólidos platónicos y la Merkaba

El poliedro estrella que ahora se llama Merkabah está compuesto por dos tetraedros. Por eso se llama estrella tetraédrica.
La merkabah se define por la esencia de su nombre. Según la terminología egipcia, se compone de tres palabras: MER, la luz celeste, KA, el cuerpo energético, y BA, el alma encarnada. La palabra Merkabah (o Merkavah) es, por tanto, un término egipcio y, posteriormente, hebreo.
En la Cábala, adquirió el significado de vehículo o carro y se asoció al viaje interior. El misticismo judío y la cábala tienen sus orígenes en el antiguo Egipto.
Comparado con un vehículo energético, el Merkabah puede ayudar a nuestro cuerpo, mente y alma a acceder y experimentar otros niveles de conciencia o potencial vital.
Un cristal Merkaba aparece como un tetraedro estelar; una estrella tridimensional de 8 puntas formada por dos pirámides triangulares, una apuntando hacia arriba y la otra hacia abajo. Se valoraba y utilizaba en muchas culturas y religiones, entre ellas la egipcia y la judía.
Un cristal Merkaba es una herramienta eficaz que se puede utilizar de muchas maneras diferentes para ayudarle a alcanzar su pleno potencial. Puede estar compuesto por diferentes cristales con poderosas propiedades curativas y de limpieza energética.
Cuando se utiliza en la meditación, un cristal Merkaba le permite experimentar una conciencia expandida, le conecta con su ser superior y le ayuda a experimentar estados de conciencia más elevados.
Cuando se realiza correctamente, la meditación Merkaba integra y armoniza los aspectos femeninos y masculinos de tu ser.
Un cristal con forma de Merkaba puede ser programado a través de la meditación y las intenciones.
También se pueden utilizar los cristales Merkaba:
- En las prácticas avanzadas de Reiki
- Para viajar por los reinos astrales
- Para activar y purificar el Cuerpo de Luz humano
- Para las visualizaciones Mer-Ka-Ba
Los sólidos platónicos en la historia
El descubrimiento de los sólidos es antiguo.
Entre los pueblos neolíticos de Escocia se han encontrado cientos de esferas de piedra talladas de unos cinco centímetros de diámetro, que se cree que datan de alrededor del año 2000 a.C. Algunos están tallados con líneas que corresponden a las aristas de los poliedros regulares. Aproximadamente la mitad tienen 6 mandos, pero otros van de tres a 160 mandos.

Los sólidos de Platón son antiguos y se encuentran en excavaciones de hace cientos de años. Como estas antiguas excavaciones romanas y egipcias (200 - 400 d.C.). Utilizaron el dodecaedro y el icosaedro, probablemente como dados. Su verdadero propósito sigue siendo un misterio.


El primer dodecaedro se encontró en 1739. Desde entonces, se han encontrado al menos 116 objetos similares desde Gales hasta Hungría y desde España hasta el este de Italia, la mayoría de ellos en Alemania y Francia. De 4 a 11 centímetros
Los griegos enseñaban que estos cinco sólidos eran los patrones básicos de la creación física. Cuatro de los sólidos se consideraban los patrones arquetípicos detrás de los cuatro elementos (tierra, aire, fuego y agua), mientras que el quinto se consideraba el patrón detrás de la propia fuerza vital, el éter de los griegos.
Estas formas predominaban en los cientos de petrosferas talladas prehistóricas encontradas en Escocia, más del 75% de las cuales representaban uno de los sólidos de Platón. Proceden de una época más de mil años anterior a la de los griegos. Estas mismas formas se relacionan ahora íntimamente con las disposiciones de protones y neutrones en los elementos de la tabla periódica.
Euclides y los cinco sólidos platónicos
Euclides hizo una completa descripción matemática de los sólidos platónicos en los Elementos (hacia el 300 a.C.); el último libro (Libro XIII) está dedicado a sus propiedades. Las proposiciones 13-17 de este Libro XIII describen la construcción del tetraedro, el octaedro, el cubo, el icosaedro y el dodecaedro en ese orden.
Para cada sólido, Euclides encuentra la relación entre el diámetro de la esfera circunscrita y la longitud de las aristas. En la Proposición 18, argumenta que no hay más poliedros regulares convexos. En efecto, para ser regular, un poliedro debe tener el mismo número de polígonos regulares en cada uno de sus vértices y la suma de los ángulos en los vértices de los polígonos regulares debe ser estrictamente inferior a 360°.
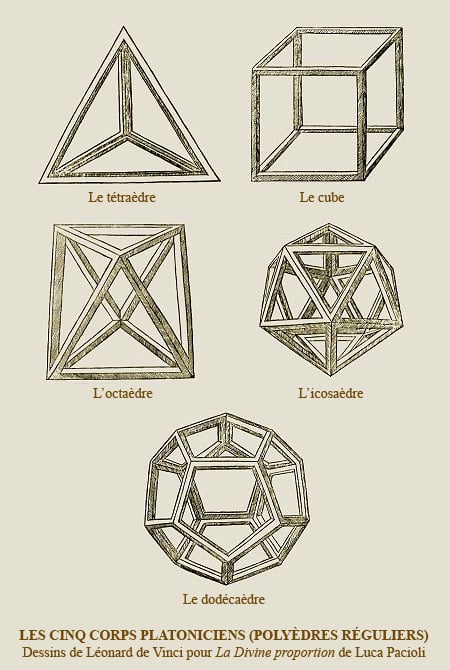
Luca Pacioli (1147-1517)
Los intereses y el talento de Luca Pacioli eran diversos. Monje franciscano, matemático y amigo de Leonardo da Vinci, con quien colaboró, enseñó matemáticas en muchas ciudades italianas.
Publicó una edición en latín de los Elementos de Euclides, pero su principal obra, "Summa di arithmetica, geometrica, proportione et proportionalita", una auténtica enciclopedia matemática, publicada en 1494, le hizo famoso.
En 1509 publicó en Venecia "De Divina Proportione", cuyo manuscrito había sido ofrecido varios años antes a Ludovico el Moro, duque de Milán. Ilustrada por Leonardo da Vinci, la obra consta de una parte principal dedicada al estudio de las propiedades de la divina proporción, seguida de un breve tratado de arquitectura, el dibujo de un alfabeto antiguo y el "Libellus", una serie de ejercicios matemáticos sobre poliedros regulares.
Cuando Pacioli estudia el número áureo en este libro, deja de ser, y no lo ha sido durante mucho tiempo, un número desconocido para las matemáticas. De hecho, su definición sigue de cerca la de Euclides.
Johannes Kepler (1571-1630)
Johannes Kepler, al igual que Pitágoras (ca. 580-495 a.C.), veía las matemáticas en todas partes, desde las vibraciones de un instrumento de cuerda hasta el movimiento de los planetas.
Kepler se interesó por el misticismo y exploró la idea del Universo como una disposición armoniosa de formas geométricas en su tratado "Mysterium Cosmographicum " (El misterio cosmográfico) de 1596 y en su tratado "Harmonices mundi " (La armonía del mundo) de 1619.





Este astrónomo alemán trató de encontrar una relación entre los cinco planetas conocidos en la época (excluyendo la Tierra) y los cinco sólidos platónicos.
En su tratado de 1596, Kepler postuló que las distancias relativas entre los seis planetas conocidos en la época podían entenderse a través de un anidamiento de los cinco sólidos platónicos, cada uno encerrado en una esfera que representaba su órbita, y la última esfera representaba la órbita de Saturno.
Desarrolló una teoría de los poliedros regulares que le permitió construir un modelo del universo. Kepler observó que los cinco sólidos platónicos podían intercalarse entre los orbes (un orbe es una esfera, o más bien, dado su grosor, un globo hueco, que contiene la órbita de una estrella) de los seis planetas conocidos en aquella época (de Mercurio a Saturno).

Estos últimos, al ser poliedros regulares, eran los sólidos que más se acercaban a la perfección divina de la esfera. Su uso en la estructura del sistema solar estaba en consonancia con la grandeza de la creación divina.
El número de estos sólidos implicaba el número de planetas: cinco intervalos, por tanto seis planetas. Pero estos poliedros también explicaban, por su disposición, las proporciones de los orbes planetarios (las distancias relativas de los planetas al Sol): cada sólido se inscribía en el orbe de un planeta y se circunscribía en el orbe del planeta inmediatamente inferior. La estructura entrelazada era la siguiente: el cubo entre las órbitas de Saturno y Júpiter, el tetraedro entre las órbitas de Júpiter y Marte, luego el dodecaedro entre esta última y la Tierra, seguido del icosaedro que encerraba el orbe de Venus, que a su vez estaba circunscrito por el octaedro, que finalmente rodeaba el orbe de Mercurio.
La idea original de Kepler resultó ser incorrecta, pero Kepler continuó con su intento de explicar el universo. De esta investigación surgió el descubrimiento de los sólidos de Kepler, la constatación de que las órbitas de los planetas no son círculos y las leyes de Kepler sobre el movimiento planetario, por las que ahora es famoso.
Los sólidos platónicos en la naturaleza
El tetraedro, el cubo y el octaedro aparecen de forma natural en las estructuras cristalinas. Esto no agota en absoluto el número de formas de cristal posibles. Sin embargo, ni el icosaedro regular ni el dodecaedro regular se encuentran entre ellos
Una de estas formas, llamada piritoedro (llamada así por el grupo de minerales con el que es típica) tiene doce caras pentagonales, dispuestas en el mismo patrón que las caras del dodecaedro regular. Sin embargo, las caras del piritoedro no son regulares, por lo que el piritoedro tampoco lo es.
Circogonia icosahedra, una especie de radiolario con forma de icosaedro regular.
A principios del siglo XX, Ernst Haeckel describió muchas especies de radiolarios, algunas con esqueletos en forma de diversos poliedros regulares. Entre sus ejemplos se encuentran el Circoporus octahedrus, el Circogonia icosahedra, el Lithocubus geometricus y el Circorrhegma dodecahedra, cuyas formas son evidentes por sus nombres.

Muchos virus, como el del herpes, tienen forma de icosaedro regular. Las estructuras virales se construyen a partir de subunidades proteicas idénticas repetidas y el icosaedro es la forma más fácil de ensamblar utilizando estas subunidades. Se utiliza un poliedro regular porque se puede construir a partir de una unidad proteica básica utilizada indefinidamente, lo que crea espacio en el genoma viral.
¿Cómo utilizar los 7 sólidos platónicos en el cristal de roca?
¿Cómo utilizar un dodecaedro?
El dodecaedro es el quinto sólido platónico. Se reconoce particularmente como la representación del universo en su conjunto o como símbolo de perfección.
Este quinto sólido es un poliedro regular convexo compuesto por doce caras pentagonales idénticas. En matemáticas, su estudio permite comprender las propiedades de la geometría en el espacio tridimensional, así como conceptos matemáticos como la geometría de los sólidos, los ángulos y las proporciones.
En adivinación, algunos practicantes utilizan dodecaedros especialmente marcados para la adivinación o la meditación. Cada cara puede representar un concepto, un elemento o una dirección. Puede utilizarse como herramienta de pensamiento o de toma de decisiones.
Los sólidos platónicos y los chakras
Dado que cada sólido platónico resuena con uno de los elementos, cada elemento también resuena a su vez con un chakra en nuestro sistema de energía. Como puedes ver, todo está relacionado entre sí.
La activación de los sólidos puede realizarse en el cuerpo humano y contribuir a :
- Reactivar la conciencia de nuestras células
- Liberar las memorias celulares
- Aumentar la tasa vibratoria y, por tanto, el potencial de autocuración a nivel físico, emocional o mental
- Restaurar la estructura y la fuerza del cuerpo de luz humano

Acuéstate durante 40 minutos con la cabeza hacia el Norte, instalando los sólidos (busca ayuda). O proceda por etapas como se indica a continuación:
- Toma el cubo y colócalo cerca de tu perineo (1er chakra).
- Vuelve a dejar el Cubo y coge el Icosaedro. Colócalo cerca de tu abdomen inferior (Chakra 2).
- Deja el Icosaedro y coge el Tetraedro. Colócalo cerca de tu plexo solar (Chakra 3).
- Deja el Tetraedro y coge el Octaedro. Colócalo cerca de tu chakra del corazón (Chakra 4).
- Deja el Octaedro y coge el Dodecaedro. Colócalo cerca de tu chakra de la garganta (Chakra 5).
- Coloca el Dodecaedro cerca de tu chakra del tercer ojo (Chakra 6).
- Coloca el Dodecaedro cerca de tu Chakra Coronal (Chakra 7). Vuelve a poner el dodecaedro en el suelo.
En cada etapa del trabajo de rearmonización, cada sólido emitirá una forma de vibración; la sensación puede variar según el individuo.
El dodecaedro representa el elemento éter y simboliza el chakra de la corona. Actúa sobre la mente y sus emociones para liberarlas. Fortalece la voluntad. Y colocar un dodecaedro cerca de ti durante la noche armoniza el sueño.
El hexaedro representa el elemento tierra y simboliza el chakra raíz. Actúa sobre el equilibrio de las personas fugitivas y evanescentes favoreciendo el arraigo.
El icosaedro representa el elemento agua y simboliza el chakra sacro. Actúa sobre las turbulencias mentales calmando la inestabilidad. Ayuda a autogestionar mejor la sexualidad.
El octaedro representa el elemento aire y simboliza el chakra del corazón. Actúa sobre los recuerdos emocionales aportando equilibrio, calma y amor. Desarrolla y fortalece el respeto por uno mismo y por los demás. Ayuda con la expresión y la sintaxis.
El tetraedro representa el elemento fuego y simboliza el chakra del plexo solar. Actúa sobre todos los cuerpos sutiles reajustando el alineamiento entre el cielo y la tierra, desatando nudos energéticos. Desarrolla la capacidad de resolver un dilema.
Uso de los sólidos platónicos para crecer espiritualmente
Hay muchas formas de usar los Sólidos Platónicos para tu crecimiento espiritual, pero la meditación es una de las formas más comunes de hacerlo. Cuando trabajas con los sólidos platónicos, estás trabajando con las energías de la creación misma. Podrás manifestar una nueva vida, una vida más alineada contigo.
Este es el verdadero significado espiritual de los Sólidos Platónicos.
Además de usarlos activamente, los Sólidos Platónicos también tienen un efecto en nuestro subconsciente, como todas las formas de Geometría Sagrada. Simplemente colocando los objetos en una habitación, equilibrarán las energías de esa zona.
Cada Sólido Platónico equilibrará las energías con las que resuena.
Descubra los significados espirituales de los Sólidos Platónicos y cómo se puede usar cada sólido para crecer espiritualmente.
El significado espiritual del cubo.
El hexaedro, o cubo, su función principal es la puesta a tierra. Puede ayudarte a reconectarte con las energías de Gaia y la Naturaleza, cimentándote firmemente. Algunos incluso dicen que podría activar tu Kundalini, si estás listo para ello.
Si estás estresado, este sólido platónico es el que mejor te puede ayudar. El Cubo puede ayudarte a eliminar la tensión y el estrés físico.
Además, proporciona la base para la creatividad y la estabilidad. Sin esta base no se estimulará la creatividad.
El significado espiritual del icosaedro
La función clave del icosaedro es la transformación. Puede ayudarte de varias maneras. Por ejemplo, mejora su proceso de pensamiento creativo. No solo eso, sino que también puede ayudarte a desbloquear y despejar bloqueos emocionales que cortan las energías creativas.
Puede ayudarte a aprender una nueva forma de vida; dejarse llevar. Permitir que la libertad de expresión, la creatividad y el cambio positivo fluyan sin esfuerzo a través de ti. Una gran manera de atraer más abundancia a tu vida.
Además, te ayudará a comprender las emociones que surgen. Te permite ver claramente por qué sientes ciertas emociones y te ayuda a reaccionar ante ellas. Es la herramienta de curación perfecta para encontrar el equilibrio y la armonía, especialmente en las áreas de fertilidad y sexualidad.
El significado espiritual del tetraedro
La función clave del tetraedro es la manifestación. Es el sólido platónico perfecto que puede ayudarte a crear un cambio en tu vida. Apoya tu poder personal y tu aceptación de lo viejo, para que puedas crear algo nuevo.
Además, puede ayudarte a pensar con mayor claridad o iluminar (elemento fuego y luz) ciertas ideas. Finalmente, el Tetraedro también traerá un equilibrio natural entre lo físico y lo espiritual. Ya que también se considera el símbolo perfecto del equilibrio y la estabilidad.
El significado espiritual del octaedro
La función clave del octaedro es la integración. Este sólido platónico puede ayudarte a sanar, aceptar, perdonar y tener compasión por ti mismo y por los demás.
El octaedro también puede ayudarte a reflexionar y elevar tu vibración. Puede ayudarlo a tener más compasión por usted mismo, lo que a su vez impulsa su proceso de curación.
También te ayudará a expresar tu creatividad a través de tu voz y te ayudará a hablar desde tu corazón. Crea una conexión más fuerte con tu mundo interior y tu mundo exterior. “Como adentro, así afuera”.
El significado espiritual del dodecaedro
Las funciones clave del dodecaedro son la ascensión, la expresión, la creación divina de la vida y la forma más elevada de conciencia.
Puede ayudarte a elevar tu frecuencia y conectarte con dimensiones superiores y tu yo superior. Es la herramienta perfecta para la meditación.
Además, el dodecaedro tiene una frecuencia muy alta. Esto no solo ayuda a elevar tu propia frecuencia, sino también la frecuencia del entorno.
Los sólidos platónicos en la geobiología
La activación de los sólidos en geobiología permite tratar en particular :
- La contaminación electromagnética
- Las diferentes redes telúricas o cósmicas-telúricas (Curry, Harthman)
- Los manantiales subterráneos
- Los recuerdos de las paredes, la presencia de entidades
Son aliados formidables en la armonización y la protección de los lugares de vida o de trabajo
Otros usos de los sólidos platónicos
Puedes llevar un sólido de cristal de roca adicional como colgante.
Puede colocar un sólido de cristal en su agua potable para informar al agua e integrar esta información cuando la beba (recuerde limpiar su sólido previamente, en un disco armonizador Flor de la vida por ejemplo).
Puede colocar un sólido de cristal (un poco más grande) en su casa u oficina para rearmonizar el espacio. Puede seleccionar el sólido según su elección y lo que desee transformar.
También puede utilizar los sólidos de Platón en la radiónica, para enviarse a sí mismo o a otra persona información beneficiosa a distancia.
La última palabra
La búsqueda de la regularidad y la armonía es una antigua búsqueda de la mente humana.
Los sólidos platónicos, o poliedros regulares, impregnan muchos aspectos de nuestro mundo. Aparecen en los cristales, en los esqueletos de animales marinos microscópicos, en los juguetes de los niños y en el arte. Han sido estudiados por muchos filósofos y científicos como Platón, Euclides y Kepler. Son de gran interés en la geometría clásica, como la obra de Euclides, que se centra en las propias figuras. También desempeñan un papel muy interesante en la geometría moderna.
Por cierto, desde Euclides no se han descubierto nuevos poliedros regulares convexos. ¡De hecho, se puede demostrar que sólo hay 5!
Este es el final de este artículo. Espero que te haya gustado, no dudes en comentar, compartir y suscribirte a nuestro boletín para estar informado de futuros lanzamientos.
Suscríbase a nuestro boletín de noticias
Y si quieres ir más allá en el descubrimiento de los símbolos, bienvenido a este espacio/tienda dedicado a la geometría sagrada. Encontrarás una multitud de mandalas fractales.
Fuentes :
Géométrie sacrée, Éditions Véga
Le pouvoir des symboles, Éditions Trajectoire
https://fr.wikipedia.org/wiki/Johannes_Kepler















 No, no todo es un mensaje del universo
No, no todo es un mensaje del universo
 El comercio independiente sacrificado por el Estado
El comercio independiente sacrificado por el Estado
 El Octágono: símbolo de justicia divina y equilibrio
El Octágono: símbolo de justicia divina y equilibrio
 Calendario de las 13 lunas: ¿un regreso a lo natural o un mito moderno?
Calendario de las 13 lunas: ¿un regreso a lo natural o un mito moderno?
 Simbolismo de la mariposa luna: metamorfosis interior
Simbolismo de la mariposa luna: metamorfosis interior