The Fibonacci sequence

The Fibonacci sequence, named after Leonardo Fibonacci, also known as Leonardo of Pisa, is a fascinating sequence of whole numbers that has found its way into fields ranging from mathematics to architecture. This 13th-century Italian mathematician introduced the Fibonacci sequence in his "Liber Abaci", a manuscript that has survived the passage of time to allow us to delve into the mysteries of this particular sequence. At the crossroads of mathematics, art and nature, the Fibonacci sequence has become an inexhaustible source of inspiration for many fields, illustrating the presence of fascinating motifs such as the golden spiral and exponential growth.
"One cannot understand the universe if one does not first apply oneself to understanding its language and knowing the characters with which it is written. It is written in the mathematical language."

Who is Leonardo Fibonacci?
Leonardo Fibonacci (c. 1175 in Pisa - c. 1250) was an Italian mathematician.
At the time, his common name was "Leonardo Pisano" (he is still known in French as Léonard de Pise), and he sometimes called himself "Leonardo Bigollo" (bigollo meaning "traveller" in Italian).
Although he is best known for the Fibonacci sequence, he played a particularly important role in linking Arab mathematical knowledge, particularly Indo-Arabic numerals, with the West.
His best-known publication is undoubtedly the Liber abaci (also written Liber abbaci), published in 1202.


The Book of Calculations is a treatise on calculations and accounting based on the decimal calculus at a time when all of the West was still using Roman numerals and abacus calculations. The book is strongly influenced by his childhood in the southern and eastern Mediterranean, and is written partly from right to left.
With this publication, Fibonacci introduced to Europe the Indo-Arabic notation system imported from India by the Arab-Muslim invasions. This system was more powerful and faster than Roman notation, and Fibonacci was fully aware of this.
The invention was initially poorly received, as the public no longer understood the calculations made by merchants. In 1280, Florence even banned the use of Arabic numerals by bankers. The zero was seen as so confusing and difficult that they called the system cifra, which derives from the Arabic name for zero (al sifr = void, zero). It is said that the use of numbers in the cabalistic tradition gave the word cipher its meaning of secret code.
Fibonacci is best known today for one of his problems leading to the numbers and sequence that bear his name, but in his day, it was above all the applications of arithmetic to commercial calculation that made him famous: calculating the profit of transactions, conversion between currencies of different countries using different bases (base 10, 12, 20).
His work on number theory was ignored during his lifetime, but was widely read over the following two centuries. His work is now widely used in market finance, and particularly in technical analysis.
Definition of the Fibonacci sequence
The Fibonacci sequence, Fib, begins with the first two terms, 0 and 1, and each subsequent term is the sum of the two preceding terms, according to the function Fib(n) = Fib(n-1) + Fib(n-2). The Fibonacci sequence can also be expressed by the mathematical formula, where the upper index term n is determined by the following relationship. These first terms of the sequence represent the initial pair of rabbits, symbolizing the growth of a population over the months.
An example of a feasible application of the Fibonacci sequence is to model the growth of a population over successive months, illustrating a progression following an arithmetic sequence. The evolution of this sequence can be visualized as a quarter circle, or even used to answer questions of divisibility or efficiency in various recreational problems. The Fibonacci sequence also branches out into fields such as architecture, where the relationship between sides and lateral lengths follows a mathematical harmony.
Leonardo da Pisa, the author of numerous manuscripts, left an indelible legacy with the Fibonacci sequence, becoming a key to harmony in mathematical modeling in dynamics, a little numerical poem that unfolds end-to-end, and a model for biological figures, such as the snail's shell. All the sequences, including Pascal's triangle, intertwine with the Fibonacci sequence, demonstrating the depth of its relationships in the vast field of mathematics.

What is the law in the Fibonacci sequence?
The Fibonacci sequence follows a law of recurrence defined mathematically by the following relationship:
F(n)=F(n-1)+F(n-2)F(n)=F(n-1)+F(n-2)
with initial conditions F(0)=0F(0)=0 and F(1)=1F(1)=1. This relationship expresses that each term of the sequence is the sum of the two preceding terms.
The explicit formula for calculating the n-th term of the Fibonacci sequence without needing to calculate all the intermediate terms is also based on a mathematical law, using the golden ratio (ϕ):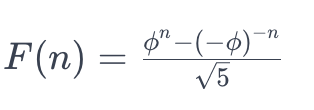
where ϕ is the golden ratio, approximately equal to 1.618033988749895.
The Fibonacci sequence also has some interesting properties linked to the golden ratio and the golden spiral. For example, as nn becomes very large, the ratio between two successive terms of the Fibonacci sequence converges to the golden ratio (ϕ).
In summary, the fundamental law in the Fibonacci sequence is the recurrence relation that defines each term in terms of the two preceding terms. This simple law generates a sequence of numbers with fascinating mathematical properties and a wide range of applications.
What's the link between the golden ratio and the Fibonacci sequence?
The link between the golden ratio (or golden spiral) and the Fibonacci sequence is closely related to the way in which the Fibonacci sequence converges towards the golden ratio as you progress through the terms of the sequence. The golden ratio, often represented by the Greek letter φ (phi), is an irrational value of approximately 1.618033988749895. This number has unique mathematical properties, and is often associated with aesthetically pleasing proportions in art, architecture and nature.
The link between the golden ratio and the Fibonacci sequence is illustrated by the following relationship: as we take successive terms of the Fibonacci sequence and divide each term by its predecessor, the resulting value converges to the golden ratio. Formally, this can be expressed by the limit: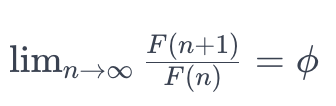
In this equation, F(n)F(n) represents the nth term of the Fibonacci sequence. This property of convergence creates pleasing length ratios and geometric patterns that are often observed in nature and used in art and architecture. For example, the golden spiral, formed by adding squares whose sides follow the Fibonacci sequence, features growth based on the golden ratio, creating an aesthetically pleasing spiral.
In short, the link between the golden ratio and the Fibonacci sequence lies in the convergence of the ratios between successive terms of the sequence towards the value of the golden ratio, giving rise to harmonious and aesthetically pleasing patterns.
In the Fibonacci sequence, the ratio of every two successive terms converges towards phi. Yet the Italian mathematician never specifically addressed the golden ratio.
To visualize this phenomenon, let's note that each successive value of this ratio gets closer and closer to phi:
1/1 = 1.000000
2/1 = 2.000000
3/2 = 1.500000
5/3 = 1.666667
8/5 = 1.600000
13/8 = 1.625000
21/13 = 1.615385
34/21 = 1.619048
55/34 = 1.617647
89/55 = 1.618182
144/89 = 1,617978
233/144 = 1.618056
377/233 = 1.618037
987/610 = 1.618033
In fact, 400 years passed before Johannes Kepler established an explicit link between the two. He was the first to mention clearly in a 1609 letter that the ratios of successive terms in the Fibonacci sequence approximate the golden ratio.
What is the limit of the Fibonacci sequence?
The Fibonacci sequence has no finite limit, because its terms increase indefinitely as the sequence progresses. Mathematically, this can be expressed by saying that the limit of the Fibonacci sequence as n tends to infinity does not exist as a finite number.
Formally, the definition of the Fibonacci sequence is given by the following recurrence relation: F(n)=F(n-1)+F(n-2)F(n)=F(n-1)+F(n-2), with initial conditions F(0)=0F(0)=0 and F(1)=1F(1)=1.
If we examine the terms of the sequence, we see that they increase indefinitely. This means that, as n becomes larger and larger, the values of F(n)F(n) will continue to grow without reaching a finite limit.
In mathematical notation, this can be expressed as :
![]()
This indicates that the Fibonacci sequence diverges towards infinity as n tends towards infinity. This is an important feature of this sequence, and reflects the exponential growth of the terms in the sequence.
Fibonacci mathematical sequence: the example of rabbits
In his book, Fibonacci also presents a simple numerical sequence based on a theoretical problem of multiplying a population of rabbits. This sequence, the basis of an incredible mathematical relationship underlying Phi, which Indian mathematicians knew as early as the 6th century, was introduced to the West by Fibonacci.
The Fibonacci sequence can be explained using the following example. Assume two newborn rabbits, one male and one female. Let's assume that the rabbits are able to mate at the age of 1 month, so that at the end of her second month of life, the female will produce two rabbits. Let's assume that our rabbits never die, and that the female produces two more rabbits (one male, one female) every month from her second month of life.
Fibonacci wondered how many rabbits we'd end up with in a year. The answer is 144, which is the 12th number in the growth sequence below, corresponding to the 12th month of new rabbits.

Starting from 0 and 1, each new term in the sequence is simply the sum of the two preceding it:
0 + 1 = 1
1 + 1 = 2
2 + 1 = 3
3 + 2 = 5
5 + 3 = 8
8 + 5 = 13
... etc., leading to the following sequence, known as the Fibonacci sequence:
0,1, 1, 2, 3, 5, 8, 13, 21,34, 55, 89, 144, 233, 377, 610, 987..
Fibonacci spiral
If you look up Fibonacci sequences on the Internet, you're bound to come across images of Fibonacci spirals or gold spirals. You've also seen this spiral superimposed on everything from the Parthenon to Mona Lisa to Donald Trump's hairline.
Typically, the spiral is created by taking a golden rectangle as a base. Divide the golden rectangle into its golden point and you'll have a square and another, smaller golden rectangle. Do the same over and over again with the smaller golden rectangle to create the image below.
And by tracing an arc through each square, you get the golden spiral.


For a related spiral, the Fibonacci spiral, we use squares whose side lengths are equal to the terms of the Fibonacci sequence, instead of creating a successive pattern of golden rectangles.
Technically speaking, these are not spirals, but scrolls. The difference is virtually imperceptible, but a true spiral is a single, equiangular (in other words, logarithmic) spiral that develops at a constant rate. In the illustration below, the green spiral is constructed by a succession of independent arcs in each square. The red spiral is a true logarithmic spiral, with the golden section every 90 degrees (equiangular spiral). Overlapping parts are in yellow.

What is the Fibonacci sequence used for and when? Applications.
The Fibonacci sequence is of great importance in many fields, and is used for a wide variety of purposes.
Here are just some of the applications and uses of the Fibonacci sequence:
- Growth and population modeling: The Fibonacci sequence can be used to model the growth of a population, particularly in situations where each generation is dependent on previous generations.
- Financial analysis: Aspects of the Fibonacci sequence are used in the technical analysis of financial markets to identify potential support and resistance levels.
- Art and design: The gold spiral, which is related to the Fibonacci sequence, is used in art and design to create aesthetically pleasing proportions. Artists and architects have incorporated these proportions into their works to create visual harmony.
- Computer science and algorithms: The Fibonacci sequence is used in computer science, particularly for recursive algorithms and dynamic programming problems. The fib function is often used as an example to teach recursion in computer science.
- Cryptography: Some cryptographic algorithms use properties of the Fibonacci sequence to generate random numbers.
- Biology: Some biological models rely on the Fibonacci sequence to describe the growth of certain structures, such as flower petals or snail shells.
- Pure mathematics: The Fibonacci sequence is studied in pure mathematics to understand its properties and behaviors. It is also used to illustrate various mathematical concepts to students.
In short, the Fibonacci sequence not only has mathematical significance, but also has applications in many fields, from art and biology to finance and computing. Its ubiquity demonstrates the beauty and versatility of this numerical sequence.
The Fibonacci sequence in nature
The Fibonacci sequence is frequently observed in nature, illustrating how mathematical patterns can manifest themselves in the living world. Many examples demonstrate the presence of this sequence in various biological structures, shapes and natural phenomena. Here are just a few examples of the Fibonacci sequence in nature:
- Arrangement of leaves on a stem: In many plants, the arrangement of leaves on a stem follows the Fibonacci sequence. Leaves generally grow in such a way as to maximize exposure to sunlight and avoid the shade of neighboring leaves, creating a spiral arrangement that conforms to the Fibonacci sequence.
- Spirals in pine cones: The spirals present on pine cones often follow the Fibonacci sequence. Seeds are arranged in spirals to maximize space while maintaining uniform distribution.
- Snail and mollusc shells: The shells of some snails and molluscs follow the shape of a logarithmic spiral, which is related to the Fibonacci sequence. This structure enables the animal to create a shell efficiently, while ensuring continued growth.
- Flowers and petals: The number of petals in many flowers often follows Fibonacci sequences. For example, daisies may have 21, 34 or 55 petals, numbers that correspond to successive terms in the Fibonacci sequence.
- Tree branching: The branching of tree branches can also follow patterns based on the Fibonacci sequence. Branches divide in such a way as to maximize the efficiency of capturing sunlight.
- Scales on certain fruits and vegetables: The arrangement of scales on certain fruits, such as pineapples, sometimes follows the Fibonacci sequence, creating interesting geometric patterns.
The presence of the Fibonacci sequence in these natural structures suggests that this numerical sequence offers optimal solutions for growth and distribution processes in the plant and animal kingdoms. It's a testament to the beauty of mathematics in the design of nature.



The Fibonacci sequence in art and architecture
The Fibonacci sequence and its mathematical properties also influence the field of art, where it is used to create aesthetically pleasing and harmonious works. Artists have explored the presence of the Fibonacci sequence in various art forms, from painting to sculpture to architecture. Here are just a few of the ways in which the Fibonacci sequence is expressed in art:
- Proportions and ratios: Proportions based on the Fibonacci sequence, notably the golden ratio, are often used to determine the size and arrangement of elements in a work of art. These ratios are considered aesthetically pleasing and have been used in famous artistic compositions.
- Golden spirals: The golden spiral, derived from the Fibonacci sequence, is used in the creation of spiraloid patterns in art. Artists have incorporated these spirals into paintings, sculptures and graphic works to create a harmonious visual dynamic.
- Mosaics and tiles: Some mosaic and tile patterns follow the proportions of the Fibonacci sequence. These patterns create a pleasing visual effect and are used in decorative art, architecture and interior design.
- Frescoes and murals: Artists use the Fibonacci sequence to determine the size of elements in frescoes and murals, creating balanced, aesthetically satisfying compositions.
- Photography and visual composition: Photographers sometimes use the Fibonacci sequence to compose images in an eye-catching way that creates visual harmony. Proportions based on the Fibonacci sequence can be applied to guide the viewer through an image.
- Architecture: Some architects incorporate the Fibonacci sequence into the design of buildings and structures. Proportions based on the Fibonacci sequence can be used to determine floor heights, window widths and other architectural elements.
The use of the Fibonacci sequence in art demonstrates how mathematical concepts can inspire artistic creation and contribute to visual perception. It provides artists with a structured framework for expressing beauty and harmony in their work.

The Fibonacci sequence in music
Although the Fibonacci sequence is not directly used in musical composition in the same way as it is in mathematics, its influence can be seen in harmonic concepts and structures. Musicians and composers have sometimes explored ideas related to the Fibonacci sequence to create patterns and structures in music. Here are just a few ways in which the Fibonacci sequence can be present in music:
- Rhythms and durations: Some composers experiment with rhythmic patterns based on the Fibonacci sequence. Note durations can follow sequences reminiscent of the progression of the sequence, adding a mathematical dimension to the rhythmic structure.
- Compositional structures: Some musicians have used the principles of the Fibonacci sequence to determine the structure of their compositions. For example, the arrangement of sections in a musical work may follow proportions based on the Fibonacci sequence, creating an interesting harmonic and melodic progression.
- Frequencies and intervals: Harmonic relationships in music, such as the interval ratios between notes, can be influenced by mathematical concepts such as the Fibonacci sequence. Although it may not always be explicit, the quest for consonance and dissonance in music can be linked to numerical relationships inspired by mathematical patterns.
- Musical forms: Some composers have explored musical forms that reflect the properties of the Fibonacci sequence, creating compositions that evolve organically and naturally.
- Use of numerical sequences: Some experimental musicians incorporate numerical sequences, including the Fibonacci sequence, into the creation of melodic and harmonic patterns. These sequences can influence the progression of the music in a way that evokes mathematical patterns.
Although the Fibonacci sequence is not a central element of musical composition, it can serve as inspiration for artistic and structural choices. Musicians interested in the relationship between mathematics and music can incorporate elements of the Fibonacci sequence to add a conceptual and intellectual dimension to their work.
The Fibonacci sequence and sacred geometry
Although the Fibonacci sequence is not intrinsically linked to sacred geometry, its mathematical properties, in particular the golden ratio, have been associated with concepts of harmonious proportions and have sometimes been incorporated into interpretations of sacred geometry.
Here's how the Fibonacci sequence can be linked to sacred geometry:
- The Golden Spiral: The golden spiral, which can be derived from the Fibonacci sequence, is sometimes considered a sacred geometric form. This spiral appears in natural patterns such as snail shells, galaxies, and even in certain artistic and architectural motifs. Some practitioners of sacred geometry see the golden spiral as a symbol of growth, evolution and harmony.
- The Golden Number (Phi): The golden ratio, often noted by the Greek letter phi (φ), is derived from the Fibonacci sequence. It is defined as the limit of the ratio between two successive terms of the sequence as n tends to infinity. The golden ratio is considered an aesthetically pleasing and balanced proportion, and is associated with concepts of beauty in sacred geometry.
- Harmonious proportions: Proportions derived from the Fibonacci sequence, in particular the golden ratio, are sometimes used to create geometric shapes in sacred geometry practices. For example, dividing a segment using the golden ratio can be seen as a search for balanced, meaningful proportions.
Famous applications of the Fibonacci sequence
The Fibonacci sequence and its mathematical properties have inspired many artists over the centuries. Here are just a few famous examples of how the Fibonacci sequence has been used in art:
- The Birth of Venus - Sandro Botticelli: This famous Italian Renaissance painting features proportions based on the Fibonacci sequence, particularly in the arrangement of the painting's elements. The shells and flower petals on the ground follow spiral patterns reminiscent of the golden spiral.
- The Mona Lisa and Vitruvian Man - Leonardo da Vinci: Leonardo da Vinci, who was fascinated by harmonious proportions, used the Fibonacci sequence in some of his works, including The Mona Lisa. Some believe that the composition of Mona Lisa's face follows proportions based on the Fibonacci sequence.
- The Parthenon - Phidias: Although the Parthenon does not date from the time of the Fibonacci sequence, the architect Phidias is said to have used proportions based on the sequence in the design of the temple. The columns and dimensions of the Parthenon reflect ratios that evoke the Fibonacci sequence, and the pediment is inscribed in a rectangle whose adjacent sides have the golden ratio.
- The golden spiral in the work of Salvador Dalí: The famous surrealist painter Salvador Dalí incorporated the golden spiral, derived from the Fibonacci sequence, into some of his works. For example, "The Sacrament of the Last Supper" features a golden spiral that guides the eye through the composition.
- Architecture by Le Corbusier: Architect Le Corbusier applied the proportions of the Fibonacci sequence in some of his architectural designs. His use of the golden ratio can be seen in buildings such as the Notre-Dame-du-Haut chapel in Ronchamp.
- Music by Béla Bartók and Iannis Xenakis: Although Béla Bartók was not directly inspired by the Fibonacci sequence, some musicologists have identified musical structures in his compositions that seem to reflect similar mathematical patterns, evoking the idea of harmonious proportions. Composer Iannis Xenakis used the Fibonacci sequence several times: as early as 1952, when he tried to create an "auditory image" of this series, and then in a number of compositions: Zygia in 1952 and Le Sacrifice in 195353.
These examples illustrate how artists, whether painters, sculptors, architects or musicians, have explored the principles of the Fibonacci sequence to create aesthetically pleasing and harmonious works. The fascination with mathematical patterns in art shows how the beauty of proportion can transcend creative disciplines.



What's the point of knowing the Fibonacci sequence?
If our eye is attracted to beauty, it's not by chance!
The ancient Greeks and Renaissance architects used phi extensively to establish the proportions of the dimensions of buildings that amaze us, and sometimes even for the proportions of a simple door or window.
We only have to look at certain buildings to understand that phi is more than just an arithmetical concept: it's at the root of beauty.
The Fibonacci sequence can be found in nature, and indeed all around us (see our article on the golden ratio).
The unique characteristics of the golden ratio have captured the imagination of countless mathematicians, painters, designers, biologists, chemists and even economists. The golden ratio is reflected in some of the greatest works of art and architecture created in the course of human history. Not everything is based on the golden ratio, but it appears in a truly astonishing multitude of places.
And most of all, it affects our perception of beauty. For some, this beauty centers on its unique mathematical and geometric properties, or its ability to create a perfectly formed fractal pattern. For others, it is perceived, consciously or unconsciously, in the beauty of nature, as well as in the human face and body. For still others, intentionally or not, it is expressed in their works of art and creative designs.
And finally, the most important question you need to ask yourself is how and why you perceive beauty, why you have the innate ability to see beauty and why you also have the need to express it.
Our soul simply needs beauty to nourish and develop.
Just as our body needs to nourish itself with healthy, balanced food, our soul, our heart, our true being, needs to surround itself with harmonious, luminous objects.
And that's why we've developed all the sacred geometry items you'll find in our online store!
If you liked this article, feel free to comment, share and subscribe to our newsletter to be informed of future issues.
Subscribe to our newsletter!
Sources:
Le nombre d'or, Editions Dervy











 Symbolism of the Luna Moth: An Inner Metamorphosis
Symbolism of the Luna Moth: An Inner Metamorphosis
 Which protection necklace should you choose?
Which protection necklace should you choose?
 Christmas Tree Star: The True Meaning
Christmas Tree Star: The True Meaning
 Meaning of the Infinity Symbol: A Journey Toward Eternity
Meaning of the Infinity Symbol: A Journey Toward Eternity
 Symbolism of the circle: the mystery of a perfect shape
Symbolism of the circle: the mystery of a perfect shape
Ed Ma - 11/16/2024 20:22:51
Bonjour, Il est intéressant de noter que dans le poème « Genèse de l’Esprit » du poète polonais du XIXe siècle, Juliusz Słowacki (1809-1849), on peut lire : "La pensée mathématique elle-même semble s’être développée dans les plantes (Myśl, zda się, sama matematyczna rozwijała się w roślinach)" et "Chaque arbre est une grande solution à un problème mathématique, un mystère de nombre(s) (Każde drzewo jest wielkim rozwiązaniem matematycznego zadania, tajemnicą liczby)" Cordialement Ed Ma P.S. Cela peut aussi vous intéresser : "Big Bang" according to the 19th century polish poet J. Słowacki